发表更新竞赛21 分钟读完 (大约3080个字)0次访问

河南大学暑假集训的日常（2）

DAY3（并查集）

HDU - 1213 How Many Tables（并查集）

RE是因为数组开小了

简单题。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
using namespace std;
const int maxn = 11000;
int T, n, m, a, b;
int f[maxn];
int ans() {
	int res = 0;
	for (int i=1;i<=n;++i) if (f[i] == i) res++;
	return res;
}
int find(int x) {return (f[x] == x) ? x : f[x] = find(f[x]);} 
int main() {
	cin >> T;
	for (int i=1;i<=T;++i) {
		cin >> n >> m;
		for (int i=1;i<=n;++i)	f[i] = i;
		for (int i=1;i<=m;++i) {
			cin >> a >> b;
			int x = find(a), y = find(b);
			f[y] = x;
		}
		printf("%d\n", ans());
	}
	return 0;
}

HDU - 3038 How Many Answers Are Wrong（带边权并查集）

image-20210805231600087

该题是一道时带边权的并查集。

对于每一个节点，不仅要维护它的祖先节点（若该节点上向右的区间有值的话右端点所对应的节点）的编号，还要维护该节点到它祖先节点的距离。

距离可以为负数，在计算区间的时候减去距离就行了。在对一组区间的数据检测是否合法的时候，检测两个端点是否可以通过某一种方式通过某一种路径联通，即两节点的祖先节点是否为同一节点。如果联通，那么就可以通过这两个节点到其祖先节点的距离来计算出这两个节点之间的距离了。

对于节点到其祖先节点的距离的维护，可以通过递归寻找祖先节点的过程中更新。在每一次寻找的过程中，如果该节点不是最终的祖先节点的话，那么将该节点到祖先节点的距离加上其父节点到祖先节点的距离。

对于新插入的节点，需要维护两节点的根节点的距离关系，可以通过画出向量的方式较为清楚的表达出来：

该笔记是针对左节点并入右节点中，若是右节点并入左节点，则将向量的方向改变一下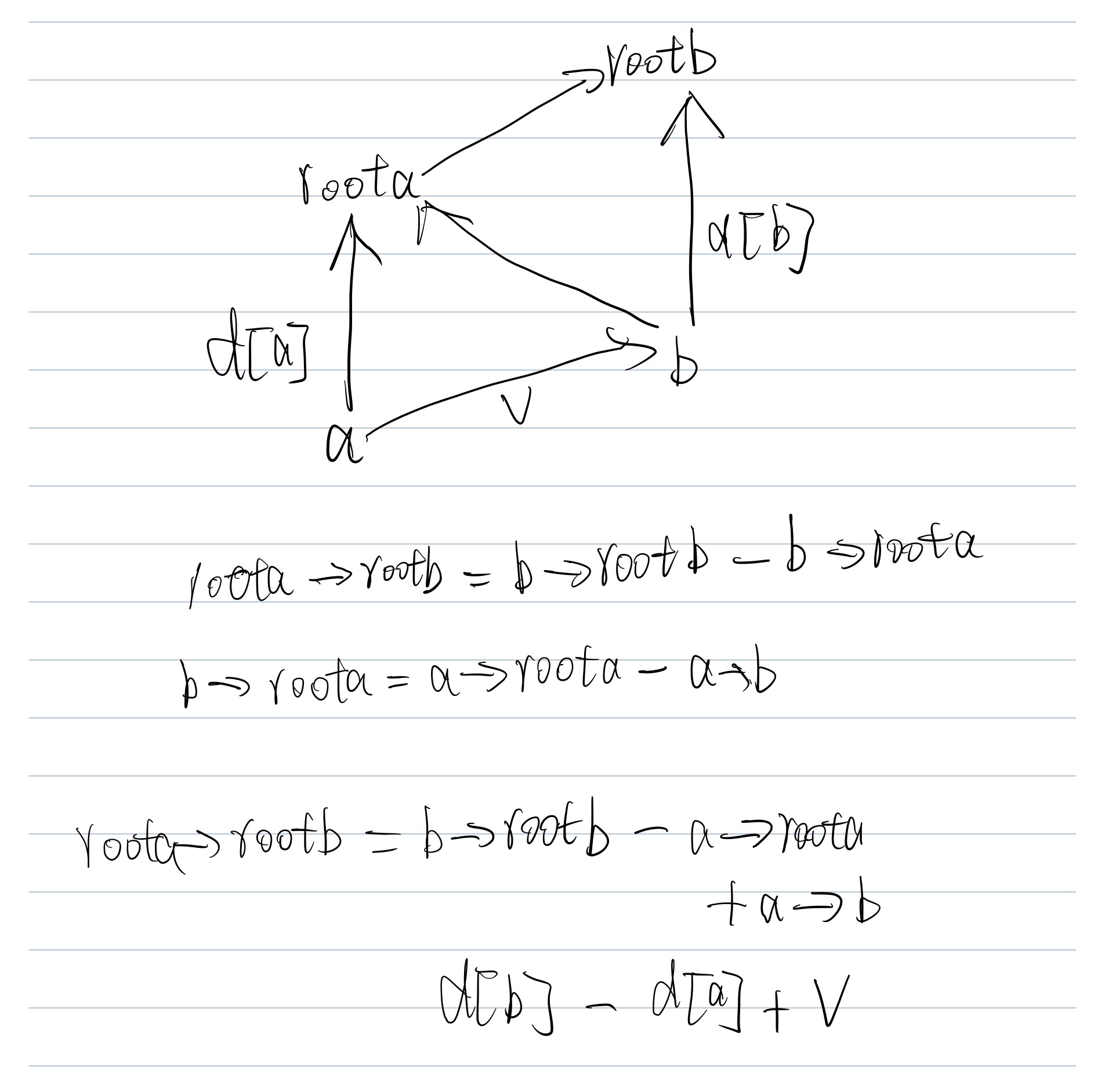

带边权并查集参考博客

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn = 200010;
int f[maxn], d[maxn];
int n, m;
int find(int x) {
	if (x != f[x]) {
		int t = f[x];
		f[x] = find(f[x]);
		d[x] += d[t];//这句话会在find函数进行递归的过程中进行更新路径上的距离值。
	}
	return f[x];
}
int main() {
	while(cin >> n >> m) {
		memset(d, 0, sizeof(d));
		for (int i=0;i<=maxn-2;++i)	f[i] = i; 
		int l, r, v, ans = 0;
		for (int i=1;i<=m;++i) {
			scanf("%d%d%d", &l,&r,&v);
			l--;
			int fl = find(l);
			int fr = find(r);
			if (fl == fr)  {
				if (d[r] - d[l] != v) ans++;
			}//这个位置没有加大括号WA了好几发，但是我现在还是不知道这里为啥需要加大括号。。。
            //这个括号到这我在HDU上WA了10+发
			else {
				f[fr] = fl;
				d[fr] = d[l] + v - d[r];
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}

POJ - 2492A Bug’s Life（种类并查集/拓展域并查集）

开两倍的f数组，x+n表示与x不相同的种类，（这种方法也叫作拆点）每一对虫子只需要保证性别不同即可，即x和y+n是联通的x+n和y也是联通的，但是x和y并不联通。如果在同一种类一侧出现了连接，即为产生了矛盾。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 2010;
int T, n, m, x, y;
bool flag = true;
int f[maxn << 1];
int find(int x) {return f[x] == x ? x : f[x] = find(f[x]);}
inline bool check(int x, int y) {
	int px = find(x), py = find(y);
	return px == py;
}
inline void unino(int x, int y) {
	int px = find(x), py = find(y);
	f[py] = px;
}
int main() {
	cin >> T;
	for (int i=1;i<=T;++i) {
		scanf("%d%d", &n,&m);
		flag = true;
		for (int i=1;i<=n*2;++i)	f[i] = i;
		for (int i=1;i<=m;++i) {
			scanf("%d%d", &x,&y);
			if (!flag)	continue;
			if (check(x, y) || check(x+n, y+n)) flag = false;
			else {
				unino(x, y+n);
				unino(x+n, y);
			}
		}
		if (!flag) printf("Scenario #%d:\nSuspicious bugs found!\n\n", i);
		else printf("Scenario #%d:\nNo suspicious bugs found!\n\n", i);
	}
	return 0;
}

POJ - 1988 Cube Stacking（带边权并查集）

这道题同样也是带边权的并查集，有点像银河英雄传说这道题。每一个节点需要维护的值有到底部的距离和该栈的元素个数。核心部分还是在合并时权值的处理。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<iostream>
#include<cstring>
#include<string>
using namespace std;
const int n = 50010;
int m, x, y;
int f[n], d[n], h[n];
inline void init() {
	cin >> m;
	for (int i=1;i<n;++i)	{
		f[i] = i;
		h[i] = 1;
		d[i] = 0;
	}
}
int find(int x) {
	if (x != f[x]) {
		int t = f[x];
		f[x] = find(f[x]);
		d[x] += d[t];
	}
	return f[x];
}
int main() {
	init();
	string od;
	for (int i=1;i<=m;++i) {
		cin >> od;
		if (od[0] == 'C') {
			cin >> x;
			find(x);
			printf("%d\n", d[x]);
		}else {
			cin >> x >> y;
			int px = find(x);
			int py = find(y);
			if (px != py) {
				f[px] = py;
				d[px] = h[py];
				h[py] += h[px];
			}
		}
	}
	return 0;
}

POJ - 1182食物链（拓展域并查集）

经典的拓展域并查集。

拓展域并查集：
首先对与最简单的并查集来说，如果两个是同一类，那么就p[pa]=pb对吧，但是对于两个相互排斥类的怎么办呢，这就涉及到拓展与并查集了，首先想法就是建立两个并查集，但是怎么把两个并查集联系起来呢？拓展个体。

这里的拓展个体是什么意思呢，一个个体我们要拆成多个，比方说两个集合存在队立关系，那么对于一个个体a，我们假设存在一个个体a+n ，a和a+n这两个是处于对立关系的，所以当我们说a和b对立的时候，意思就是在说，a+n和b在同一并查集，b+n和a在同一并查集，当我们说，a和b是同类的时候，那么也就是说a和b属于一个并查集，且a+n和b+n属于一个并查集。

开三倍的数组，除了本身的域之外拓展的两个域表示域和本身的关系。分别表示天敌和捕食。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
#define rep(i, a, n) for (ll i=a;i<=n;++i)
#define per(i, n, a) for (ll i=n;i>=a;--i)
#define IOS std::ios::sync_with_stdio(false)
#define enter putchar('\n')
typedef long long ll;
using namespace std;
const int maxn = 50010;

int n, k, f[maxn * 3];
int d, x, y, ans;
int getfa(int x) {return (f[x] == x) ? x : f[x] = getfa(f[x]);}
inline void un(int x, int y) {
	int a = getfa(x);
	int b = getfa(y);
	if (a != b) f[b] = a;
}
void work(int d, int x, int y) {
	if (x > n || y > n) {ans++;return;}
	if (d == 1) {
		if (getfa(x + n) == getfa(y) || getfa(x + 2 * n) == getfa(y)) {ans++;return;}
		un(x, y);
		un(x + n, y + n);
		un(x + 2 * n, y + 2 * n);
	}
	if (d == 2) {
		if (getfa(x) == getfa(y) || getfa(x + 2 * n) == getfa(y)) {ans++;return;}
		un(x + n, y);
		un(y + 2 * n, x);
		un(y + n, x + 2 * n);
	}
}
int main() {
	scanf("%d%d", &n, &k);
	rep(i, 1, n*3) f[i] = i;
	rep(i, 1, k) {
		scanf("%d%d%d", &d, &x, &y);
		work(d, x, y);
	}
	printf("%d\n", ans);
	return 0;
}

DAY4（树状数组）

POJ - 3468A Simple Problem with Integers（线段树/树状数组）

一个简单的区间修改和区间求和的板子题。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 7;
struct SegmentTree {
	ll l, r;
	ll dat, add;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define dat(x) tree[x].dat
	#define add(x) tree[x].add
}tree[maxn << 2];
ll a[maxn << 1];
ll n, m;
inline ll Read() {
	ll x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
inline void update(ll p) {dat(p) = dat(p<<1) + dat(p<<1|1);}
void build(ll p, ll l, ll r) {
	l(p) = l; r(p) = r;
	if (l == r) {dat(p) = a[l]; return;}
	ll mid = (l + r) >> 1;
	build(p<<1, l, mid);
	build(p<<1|1, mid+1, r);
	update(p);
}
void spread(ll p) {
	if (add(p)) {
		add(p<<1) += add(p);
		add(p<<1|1) += add(p);
		dat(p<<1) += add(p) * (r(p<<1) - l(p<<1) + 1);
		dat(p<<1|1) += add(p) * (r(p<<1|1) - l(p<<1|1) + 1);
		add(p) = 0;
	}
}
void change(ll p, ll l, ll r, ll d) {
	if (l <= l(p) && r >= r(p)) {
		dat(p) += d * (r(p) - l(p) + 1);
		add(p) += d;
		return;
	}
	spread(p);
	ll mid = (l(p) + r(p)) >> 1;
	if (l <= mid) change(p<<1, l, r, d);
	if (r > mid) change(p<<1|1, l, r, d);
	update(p);
}
ll  ask(int p, int l, int r) {
	if (l <= l(p) && r >= r(p))	return dat(p);
	spread(p);
	ll mid = (l(p) + r(p)) >> 1;
	ll res = 0;
	if (l <= mid) res += ask(p<<1, l, r);
	if (r > mid) res += ask(p<<1|1, l, r);
	return res;
}
inline void init() {
	n = Read(); m = Read();
	for (register int i=1;i<=n;++i)	a[i] = Read();
	build(1, 1, n);
}
inline void work() {
	ll l, r, d;
	char op; 
	while(m--)  {
		cin >> op;
		if (op == 'C') {
			l = Read(); r = Read(); d = Read();
			change(1, l, r, d);
		}
		if (op == 'Q') {
			l = Read(); r = Read();
			printf("%lld\n", ask(1, l, r));
		}
	}
}
int main() {
	init();
	work();
	return 0;
}

HDU - 1166敌兵布阵（树状数组）

单点修改区间求和的树状数组板子题。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
typedef long long ll;
using namespace std;
const int maxn = 50010;
int T, n, l, r;
int a[maxn], c[maxn];
string od;
inline int Read() {
	int x=0,f=1;char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
inline int ask(int x, int res = 0) {for (; x>=1; x-=(x&-x))	res += c[x];return res;}
inline void update(int x, int v) {for (; x<=n; x+=(x&-x)) c[x] += v;}
inline int query(int l, int r) {return ask(r) - ask(l - 1);}
inline void init() {
	n = Read();
	memset(c, 0, sizeof(c));
	memset(a, 0, sizeof(a));
	for (int i=1;i<=n;++i) {
		a[i] = Read();	
		update(i, a[i]);
	}
}
int main() {
	T = Read();
	for (int i=1;i<=T;++i) {
		init();
		printf("Case %d:\n", i);
		while(cin >> od && od != "End") {
			l = Read(); r = Read();
			if (od == "Add") update(l, r);
			if (od == "Sub") update(l, -r);
			if (od == "Query") printf("%d\n", query(l, r));
		}
	}
	return 0;
}

HDU - 1394Minimum Inversion Number（逆序对/树状数组）

树状数组求逆序对数的改进版，需要在题中所给的序列生成的一系列序列中找到逆序对数最小的那一组。

关于求一个数列的逆序对数，可以用树状数组来维护一个数字前面比自己大的数的个数。树状数组可以方便的在线求前缀和，所以说可以用树状数组来完成这道题。

树状数组求逆序对参考博客

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<string>
#define int ll
using namespace std;
typedef long long ll;
const int maxn = 5010;
int n, a[maxn << 2], f[maxn << 2];
int tmp, ans;
inline int lowbit(int x) {return -x&x;}
void update(int x, int v) {for (; x<=n; x+=lowbit(x))f[x] += v;}
int ask(int x, int res = 0) {for (; x>=1;x-=lowbit(x)) res += f[x];return res;}
signed main() {
	while(scanf("%d", &n) != EOF) {
		memset(a, 0, sizeof(a));
		memset(f, 0, sizeof(f));
		tmp = ans = 0;
		for (int i=1;i<=n;++i) {
			scanf("%d", &a[i]);
			a[i]++; 
			update(a[i], 1);
			tmp += (i - ask(a[i]));
		}//该过程是求一个序列的逆序对的方法
		ans = tmp;
		for (int i=1;i<n;++i) {
			tmp += (n - 2 * a[i] + 1);
			ans = min(ans, tmp);
		}//这一段是解决如何求出每一个元素后移之后的序列逆序对数
		printf("%d\n", ans);
	}
	return 0;
}

HDU - 2795Billboard（线段树）

这道题的实现其实不太难，难点是如何建树。

由题可知，我们可以在广告牌的高度上建树，然后对于每一个新的广告，查找最靠下的可以满足当前广告牌的位置插入，实际上就是维护了一个区间的最大值，来进行判断当前广告是否可以放到该区间中。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
typedef long long ll;
const ll maxn = 500010;
ll n, h, w;
ll a[maxn * 4];
inline void update(ll p) {a[p] = max(a[p << 1], a[p << 1 | 1]);}
void build(ll p, ll l, ll r) {
	if (l == r)	{
		a[p] = w;
		return;
	}
	ll mid = (l + r) >> 1;
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
	update(p);
}
ll ask(ll x, ll l, ll r, ll p) {
	if (l == r) {
		a[p] -= x;
		return l;
	}
	ll mid = (l + r) >> 1;
	ll res = 0;
	if (a[p<<1] >= x)	res = ask(x, l, mid, p<<1);
	else 	res = ask(x, mid + 1, r, p<<1|1);
	update(p);
	return res;
}
int main() {
	while(scanf("%d%d%d", &h, &w, &n) != EOF) {
		memset(a, 0, sizeof(a));
		h = min(h,n);
		build(1,1,h);
		ll x = 0;
		for (int i=1;i<=n;++i) {
			scanf("%d", &x);
			if (a[1] < x)	printf("-1\n");
			else	printf("%d\n", ask(x, 1, h, 1));
		}
	}
	return 0;
}

POJ - 2777Count Color（线段树+状态压缩）

用位运算来保存颜色的状态，加上懒惰标记，然后update维护父子节点的信息会不太一样。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<cstdio>
#include<cstring>
#include<string>
#define int ll
using namespace std;
typedef long long ll;
const int maxn = 500010;
int n, t, m, l, r, c;
int a[maxn << 2], f[maxn << 2];
char od[5];
void update(int p) {a[p] = a[p*2] | a[p*2+1];}
void spread(int p) {a[p*2+1] = a[p*2] = f[p*2+1] = f[p*2] = f[p];f[p] = 0;} 
void change(int p, int l, int r, int x, int y, int c) {
	if (x <= l && r <= y) {
		f[p] = a[p] = 1 << c;
		return;
	}
	int mid = (l + r) >> 1;
	if (f[p])	spread(p);
	if (x <= mid) change(p*2, l, mid, x, y, c);
	if (y > mid) change(p*2+1, mid + 1, r, x, y, c);
	update(p);	
}
int ask(int p, int l, int r, int x, int y) {
	if (x <= l && r <= y)	return a[p];
	ll mid = (l + r) >> 1;
	if (f[p])	spread(p);
	ll res = 0;
	if (x <= mid) res |= ask(p<<1, l, mid, x, y);
	if (y > mid) res |= ask(p<<1|1, mid + 1, r, x, y);
	return res;
}
int cnt(int x) {
	int ans = 0;
	while(x) ans++, x -= -x&x;
	return ans;
}
signed main() {
	scanf("%lld%lld%lld", &n,&t,&m);
	change(1, 1, n, 1, n, 1);
	for (int i=1;i<=m;++i) {
		scanf("%s%lld%lld", od, &l, &r);
		if (l > r)	l ^= r ^= l ^= l;
		if (od[0] == 'C') {
			scanf("%lld", &c);
			change(1, 1, n, l, r, c);
		}else printf("%lld\n", cnt(ask(1, 1, n, l, r)));
	}
	return 0;
}

河南大学暑假集训的日常（2）

https://dicemy.com/8528

作者

Dicemy

发布于

2021-08-05

更新于

2022-05-23

许可协议

喜欢这篇文章？打赏一下作者吧

评论

关于我

目录

×