数学建模入门

准备数学建模过程中的一些小小笔记

Matlab学习笔记

语法小知识：

• 同一行中间用逗号分隔，也可以不用逗号，直接用空格 分号可以用来分隔每一行的元素就是说逗号是一行中的数据，分号分割行与行之间。
• 矩阵E(:)表示矩阵的所有元素，E(:,1)表示第一列，E(1,:)表示第一行。
• 2:5表示从第2到第5，1:3:10表示从1到10，每次递增3。2:end表示从第二行到最后一行，
• ~=是不等号
• Matlab函数的声明要单独放在一个.m文件中，不能直接放在主函数里面。函数声明格式：function [输出变量] = 函数名称(输入变量） 最后用end结束声明

% 常用指令操作
clc % 清屏
clear all % 清除工作区的所有变量
hold on 
hold off % 控制图像是否被刷新
% 常用字符串函数
char(65) % ascii码对应的字符，A
length(s) % 字符串长度
strcmp() % 字符串比较函数
strcat() % 将多个字符串合并成一个
num2str() % 将数字转换为字符串
% 常用数学函数
size() % 数组大小，第二个参数也是dim表示矩阵的维度。
magic() % 生成一个幻方
abs(s) % 求s的ascii码
floor()	% 取整函数
sum() % 求和函数，辅助参数dim表示求和的维度，1表示按列，2表示按行，默认dim=1
repmat() % 复制扩展矩阵
sort() % 将数组或矩阵排序
prod() % 计算矩阵每一列的乘积
eig() % 计算矩阵的特征值
inv() % 求矩阵的逆矩阵
rand() % 产生（0,1）之间均匀分布的伪随机数组成的数组
randn() % 生成标准正态分布的伪随机数（均值为0，方差为1）
randperm() % 将一序号随机打乱，序号必须是整数
normrnd(MU,SIGMA) % 生成服从正态分布的随机数
% 常用数据输入输出函数
disp() % 向命令行输出字符或数字
input() % 从命令行读取数据
xlsread('xls_name_string') % Excel表格读取
save % 用来将数据保存为.mat文件
load % 用来加载之间生成的.mat文件
% 常用绘图函数
plot(x, y) % 创建2维直线图
stem(Y) % 绘制数据序列Y的茎状图
meshgrid(a, b) % 生成二维网格
contour3(x, y, z) % 三维等值线绘图
legend('string1','string2') % 标注绘制的图形的名称
xlabel() ylabel() zlabel() % 标注x,y,z轴
title()	% matlab绘图标题设置
set() % 设置图像属性
axis() % 对坐标轴进行缩放操作

% matlab里的一些基本规范
% 数值
% 字符串

• floor函数详解
• randperm函数详解
• normrnd函数详解
• repmat函数详解
• size函数详解
• magic函数详解
• sum函数详解
• prod函数详解
• eig函数详解
• find函数详解
• plot命令详解
• meshgrid函数详解
• contour3函数详解
• stem函数详解
• hold on 和 hold off 语句详解
• legend函数详解
• xlabel函数详解
• set函数详解
• axis函数详解
• title函数详解+matlab二维画图基本操作
• xlsread函数详解
• disp函数详解
• input函数详解
• save 和 load详解

一、矩阵及数组操作例题：

% 生成一个3x3和15x8的单位矩阵
eye(3, 3)
eye(15, 8)
% 生成全1矩阵
ones(3)
ones(15, 8)
% 全0矩阵
zeros(3)
zeros(15, 8)
% 均匀分布随机矩阵（[-1, 1]之间）
2 * rand(3, 3) - 1
2 * rand(15, 8) - 1
% 正态分布矩阵（均值为1，方差为4）
1+sqrt(4)*randn(3,3)
% 利用fix及rand函数生成[0,10]上的均匀分布的10x10的整数随机矩阵a，然后统计a中大于等于5的元素的个数。
a = fix(10*rand(10,10));
b = [a>=5];
c = [sum(b)];
sum(c')
% 在给定的矩阵中删除含有整行内容全为0的行，删除整列内容全为0的列。
a = [1 2 0 4;0 0 0 0;5 6 0 8; 9 1 0 2];
a(:,find(sum(abs(a'))==0)) = [];
a(find(sum(abs(a'))==0),:) = [] % 没看懂，该写法待确认

二、绘图：

% 在同一图形窗口画出下列两条曲线图像，并用legend标注：
x=0 : 1 : 10;
y1=2*x+5;
y2=x.^2-3*x+1;
plot(x, y1, x, y2);
legend('y1','y2')
% 画出下列函数的曲面及等高线
% z = x^2 + y^2 + sin(xy).
[x, y] = meshgrid(0:0.25:4*pi);
z=x.^2+y.^2+sin(x*y);
contour3(x, y, z);
meshc(x, y, z)

三、简单程序设计

% 求分段函数
x=input('请输入x的值：');
if x>=-3 && x < -1
    y=(-x^2-4*x-3)/2;
elseif x>=-1 && x<1
    y=-x^2+1;
elseif x>=1 && x<=3
    y=(-x^2+4*x-3)/2;
else
    y='error'
end
y
% 分数序列求和
m = 1;
n = 2;
sum = 0;
for k=1:15
    f=n/m;
    sum=sum+f;
    t=n;
    n=m+n;
    m=t;
end
sum

一些注意事项:

• 在变量定义的时候多写注释，注明每个变量的作用。
• 好的数学建模matlab的代码部分注释都很详细。
• 可以将代码分成几个部分，这样更加清晰，e.g. 数据清除，导入数据，数据预处理，相关步骤等….
• 在很多代码开头会遇到：clear;clc 这两条一起使用，起到“初始化”的作用，防止之前的结果对新脚本文件（后缀名是 .m）产生干扰。

数学建模常见算法学习

层次分析法（AHP）

一、对于一个问题，先分析系统中各因素之间的关系，建立系统的递阶层次结构（三层图）。

二、然后对于同一层次的各元素关于上一层中某一准则的重要性进行两两比较，构造判断矩阵。

在准则层需要生成每个准则的权重，在方案层需要生成对于每个准则的得分，使用两两对比的方法生成判断矩阵然后就可以计算出每个准则的权重或者方案对不同准则的得分了。

在层次分析法中我们构造的判断矩阵均是正互反矩阵(𝑎ij * 𝑎ji = 1)，若正互反矩阵满足𝑎ij * 𝑎jk = 𝑎ik，则我们称为一致矩阵。在判断矩阵计算准则的权重或者方案对不同准则的得分之前，需要对其进行一致性检验。

三、通过计算一致性指标和一致性比例来评判判断矩阵是否可以接受，计算对于该准则的相对权重。

进行一致性检验的一致矩阵准则的权重的计算或者方案对不同准则的得分的计算，计算权重或者得分有多种方式：

• 算数平均法求权重

• 集合平均法求权重

• 特征值法求权重

计算出所有的方案对不同准则的得分和准则的权重之后就可以计算每个方案的加权得分了。

四、计算各层元素对系统目标的合成权重，并进行排序。

TOPSIS法（优劣解距离法）

一、将原始矩阵正向化，将所有的指标转化成极大型指标。

• 极大型指标
• 极小型指标
• 中间型指标
• 区间型指标

二、正向化矩阵标准化。

消除不同指标量纲的影响，例如名次和分数两个指标导致的量纲不统一的影响。

三、计算得分并归一化

通过公式计算每一个评价对象对不同的评价指标离最小值的距离和到最大最小距离的和的比值来得到评价对象在该评价指标上的得分。

四、带权重的TOPSIS

通过层次分析法可以得到不同的指标的权值，在进行计算得分的时候乘以相应的权值。

插值算法

理解：感觉该算法就是通过已知的一些点来推测拟合出一个函数，并借此函数计算出需要插值的点所对应的值是多少

常见插值方法：

• 多项式插值
• 分段插值
• 三角插值

一、拉格朗日插值法

通过该方法，可以通过n+1个点来找到一个n+1项n次的一个多项式作为插值函数，来估计对应插值点的函数值。

龙格现象：高次插值会产生龙格现象，即在两端处波动极大，产生明显的震荡。在不熟悉曲线的运动趋势的前提下，不要轻易使用高次插值

分段线性插值

分段线性插值法的一种为分段二次插值法，在几何上利用分段抛物线来代替原函数，故分段二次插值法又称为分段抛物线插值法。

但是在分段时使用的插值方法本质还是拉格朗日插值法。

二、牛顿插值法

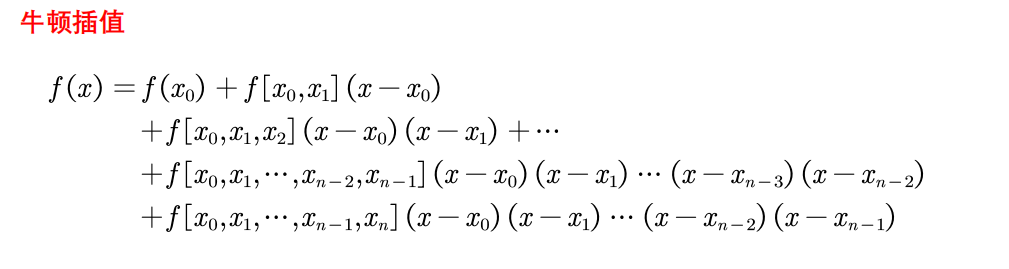
与拉格朗日插值法相比，牛顿插值法具有继承性。（牛顿插值法每次插值只和前n项的值有关，这样每次只要在原来的函数上添加新的项，就能够产生新的函数）但是牛顿插值也存在龙格现象的问题。

拉格朗日插值法和牛顿插值法两种方法得到的多项式都不能全面的反映被插值函数的形态，比如说在一个或者全部节点上的导数值，或者高阶导数值，这两种插值法都不能满足。

三、埃尔米特（Hermite）插值法

埃尔米特插值法可以保证插值函数在节点处有切线（光滑）使插值函数和被插值函数的密合程度比较好。

分段三次埃尔米特插值法

直接使用Hermite插值得到的多项式的次数也比较高，也会存在龙格现象，因此在实际应用中，往往使用分段三次Hermite插值多项式（PCHIP）

四、三次样条插值法

该插值法同样是区间插值法，是可以保证二阶连续可微的插值法。

这些插值法都在Matlab内部提供了封装好的实现方法，体现为内置的函数。