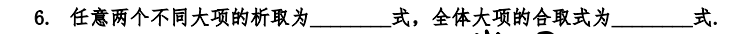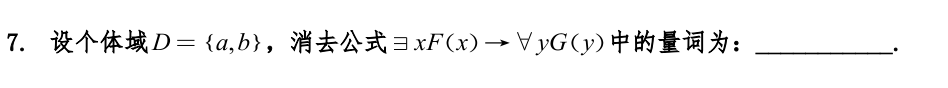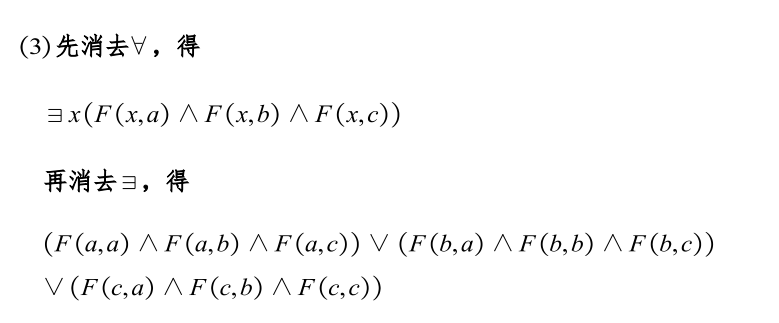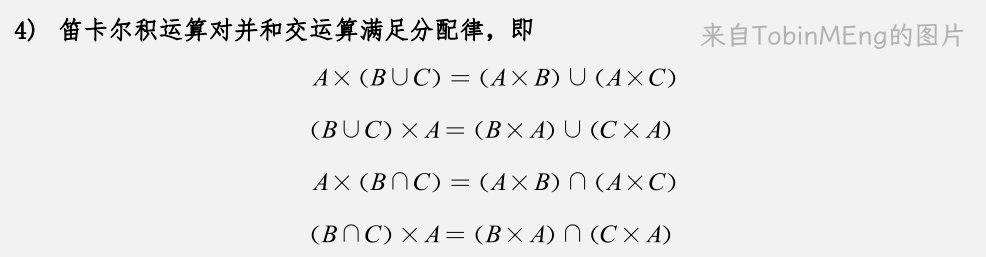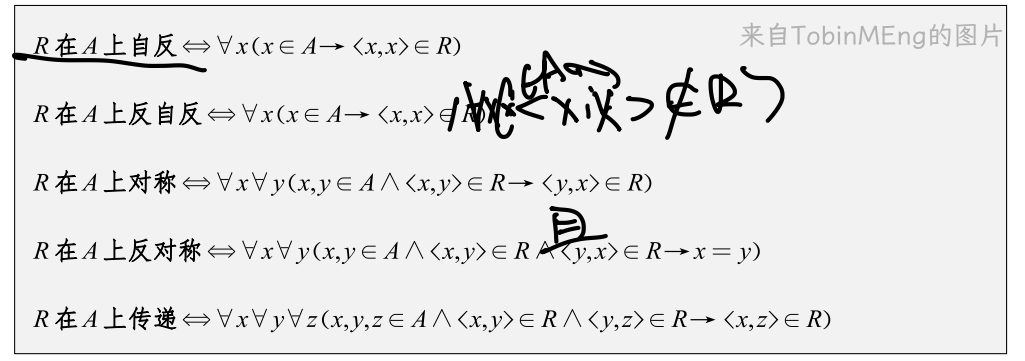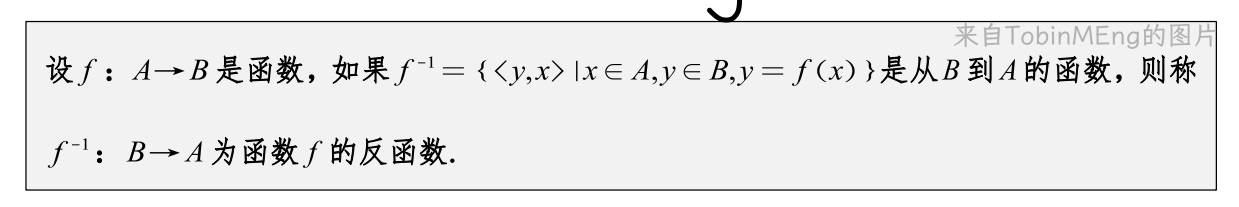离散数学复习
期末的小小总结
文件下载
课时一 命题逻辑的基本概念
1、 命题
例如:
5x + 1 > 11 这一语句不为命题。
一个未证明真伪的猜想是一个命题。
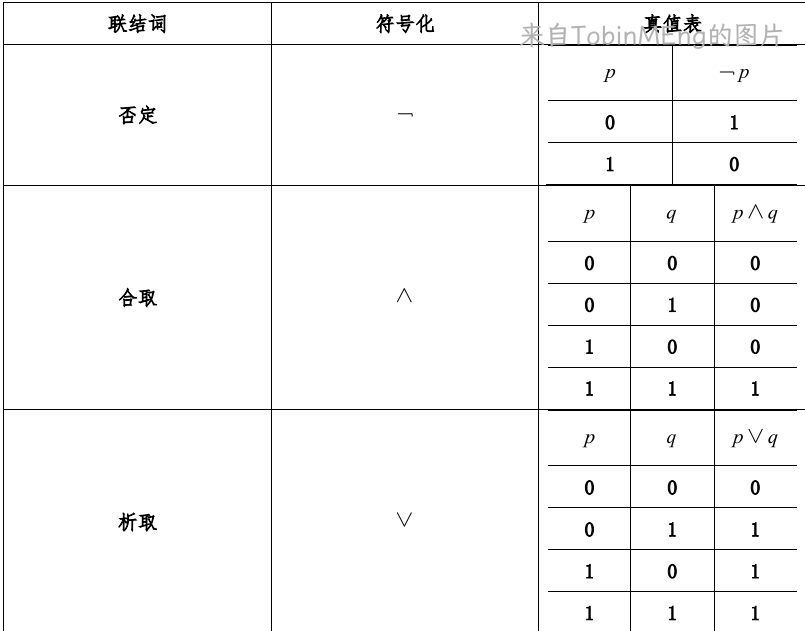
2、命题连接词
合取就是且,只有都为真才为真。
析取就是或,有一个为真就是真。
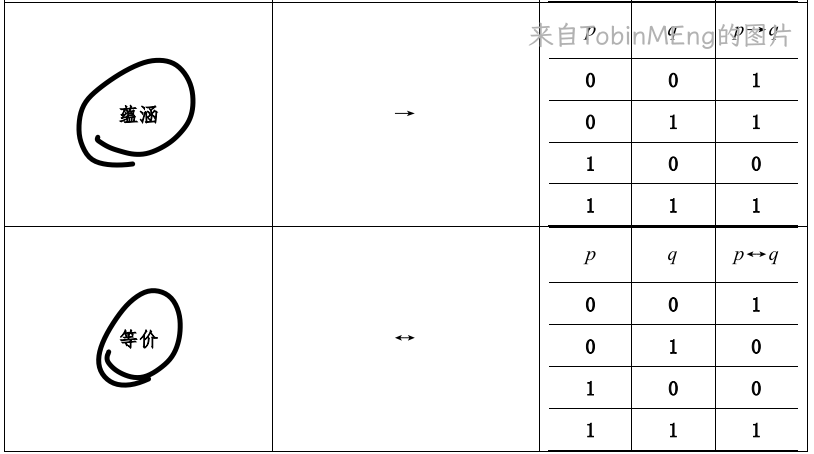
蕴含只有左1右0为假,其余都为真。
关于蕴含的实际意义,如何去理解这个关系可以看一看知乎上的回答:

image-20220214174604077
但是要注意:
另一条回答:

image-20220214174718778
等价就是两个同真同假才为真,其余为假。
将命题符号化时:
注意带有蕴含的命题符号化时,当意思中带有前者只有后者决定时,需要写为后者蕴含前者。
注意一些带有或者的命题的符号化,例如:
3、命题公式及其赋值
命题的合式公式中的每一个可以取真假值的字母叫做一个命题变元。
对于命题变元的任意赋值都为真的命题公式称为重言式或者永真式。
对于命题变元的任意赋值都为假的命题公式称为矛盾式或者永假式。
如果存在一组命题变元的赋值可以使命题为真,则称该命题为可满足式。
课时二 命题逻辑等值演算
1、 等值式
A和B中应该含有相同的命题变元。
常见等值式可以帮助命题公式的化简。
常见题型有判断命题公式为重言式或者矛盾式,或者通过等值演算证明两个命题式为等值式。
蕴含等值式和假言易位和归谬论这几个比较常用,感觉用处比较大。
仔细理解分配律,当两个括号进行分配律时可以一步一步做。直接全部展开可能会出错。
2、析取范式与合取范式
重点是:析取范式应该是几个简单合取式的析取,合取范式应该是几个简单析取式的合取。
3、主析取范式与主合取范式
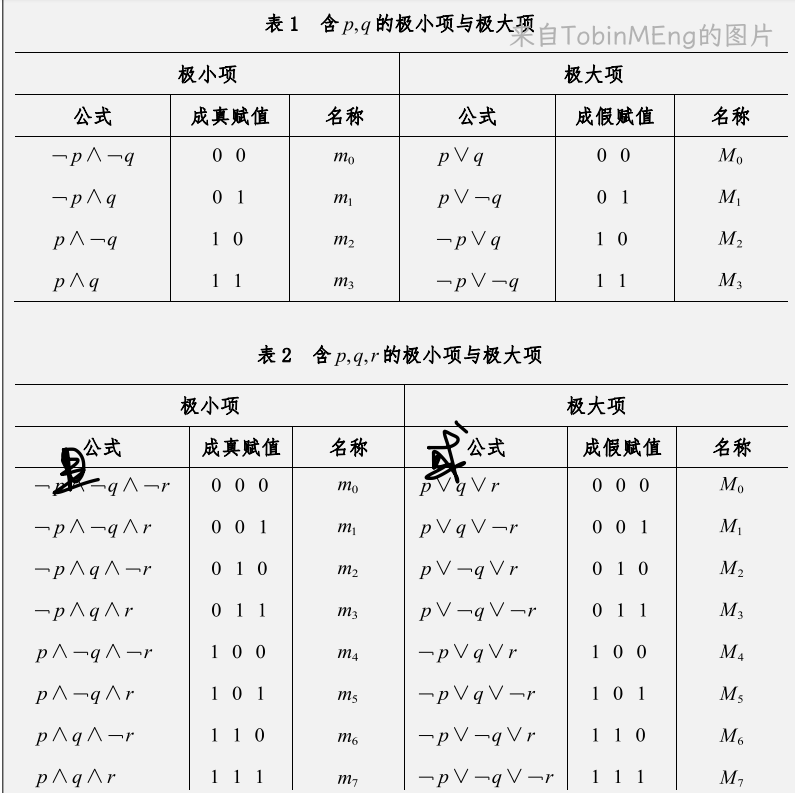
主析取范式的每一个简单合取范式成为最小项,主合取范式的每一个简单析取范式成为最大项。
一个式子的极大项和极小项的标号是从0开始,到2的n次方-1结束。
求一个式子的主析取范式和主合取范式的方式:
1、列该式子的真值表,通过真值表中的成真赋值得到该式子的极小项,从而写出该式子的主析取范式。主合取范式则反之,取真值表中成假赋值的极大项写出主合取式。
2、通过等价演算求出式子的极小项的析取范式,从而得到主析取范式。
3、通过式子已知的主合取范式来求出式子的主析取范式。(两个范式中各项的序号互补)
4、联结词的完备集
箭头向上表示两个命题的与非关系,↑可以和∧类比记忆
箭头向下表示两个命题的或非关系,↓可以和∨类比记忆
联结词完备集分为两类:
1、包含非号¬的集合中除了单独的等价关系↔不能与之构成完备集之外,其他任意若干个关联符都可以和非号构成完备集。
2、至少包含与非或者或非其中一个的联结词集合
例题:
题中的大项指的是极大项。极大项指的是简单析取式。本题答案为永真,永假。
课时三 命题逻辑的推理理论
1、推理的相关公式
其中①和②常常用于做一些小的变换,或者引入一些新的条件。
③和④常常用于一般比较简单的证明的过程中,比较重要。
⑤⑥⑦三段论使用也是比较多。
⑧和⑨使用较少。
2、自然推理系统P
例题1:
需要记住自然推理系统的推理过程,先通过前提列出所有的条件,然后列出结论。在下面通过证明过程来通过前提的一系列变化得到结论。
在证明的每一条之后都要列出通过那些条件使用那些定理得到。
在将前提引入时,需要在后面加上前提引入这样的语句。
例题2:
先将命题符号化,每一个句号就是一个前提。所以后面跟的的就是结论。
例题3:
若结论中是一个蕴含式的话,结论的前面部分的命题应该作为附加前提引入到证明过程中。
这样使用完所有的前提和结论中的附加前提之后就可以得到最后结论中蕴含式中的后部分。从而得出结论为真的结论。
例子4:
归谬法通过引入结论的否定,使得最后推出的结果和前提矛盾,即推出的结果和前提的一部分合取值为假,从而得出否定的结论错误,这样就可以证明命题必须为真了。
其实这道题通过正常的构造法也可进行证明。
课时四 谓词逻辑基本概念
1、谓词逻辑命题符号化
例子1:
例子2:
这两个例子说明在全称量词中两个谓词的关系用蕴含,但是在存在量词中两个谓词的关系用合取。
例子3:
2、谓词逻辑公式及其解释
例子1:
例子2:
说实话,没看懂这题。
看到后面的谓词逻辑的等值演算与推理看懂了。
存在量词去掉的方法就是将论域中的值都带入公式然后将每一种情况全部析取即可。
同理全称量词是每一种情况的全部合取。
这道题也没看懂。
课题五 谓词逻辑等值演算与推理
1、 谓词逻辑等值式与置换规则
我觉得应该是自由出现和限制出现搞混了。上面的自由出现的个体变项都应该改成限制出现。
对于①和②中的大部分量词辖域的收缩和扩张基本上都是直接去掉括号即可。但对于含有蕴含的谓词需要去掉括号之后改变量词。
对于3)中的式子来说,需要特殊记忆,注意有③和④公式存在顺序。
全称量词的合取有分配律
存在量词的析取有分配律
量词分配等式中含有合取符号的分配直接去括号即可。
例子1:
感受一下这种方法:
存在量词去掉的方法就是将论域中的值都带入公式然后将每一种情况全部析取即可。
同理全称量词是每一种情况的全部合取。
2、谓词逻辑前束范式
很遗憾,所有的谓词逻辑公式都存在等值的前束范式。
注意:前束范式中量词一定要在最前面,连像非号之类的符号也不应该放在量词前面。
注意2)
3、谓词逻辑的推理理论
我把这些规则称为:魔法。:crystal_ball:
③中的一些推理我觉得理解不了。
例题1:
看懂了,但是脑子说不会。:innocent:
要熟悉量词的增加和删去。其实也是量词的实际含义。
例子2:
实质就是将谓词逻辑变换成命题逻辑,然后通过命题的演绎推理得到一个命题,再将这个命题转换成谓词逻辑。(对于结论中是存在的谓词逻辑比较适用)
例子3:
对于自然语言中含有量词的命题就要考虑适用量词逻辑进行证明。
课时六 集合代数
1、集合的基本概念
注意真子集的符号
P(A)和E的含义。
2、集合的运算
对称差就是两个集合的并减去两个集合的交。
3、有穷集的计数
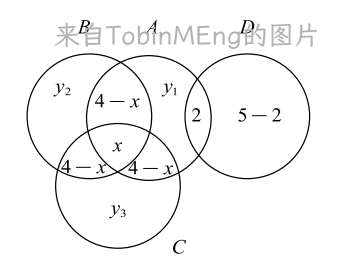
可以类似这种的文氏图帮助计算
例题1:
例题2:
4、集合恒等式
注意要进行德摩根律的特别记忆
即进行差运算和求补集运算时去括号要将交和并进行转换。
重点记忆第一个公式。进行灵活运用
课时七 二元关系
1、有序对与笛卡尔积
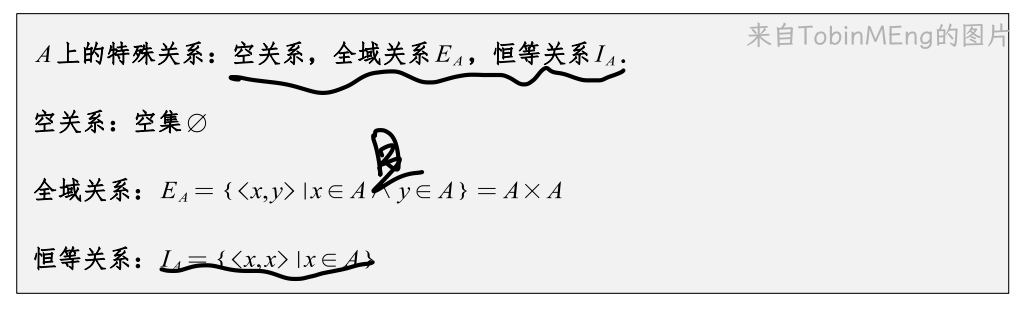
2、二元关系
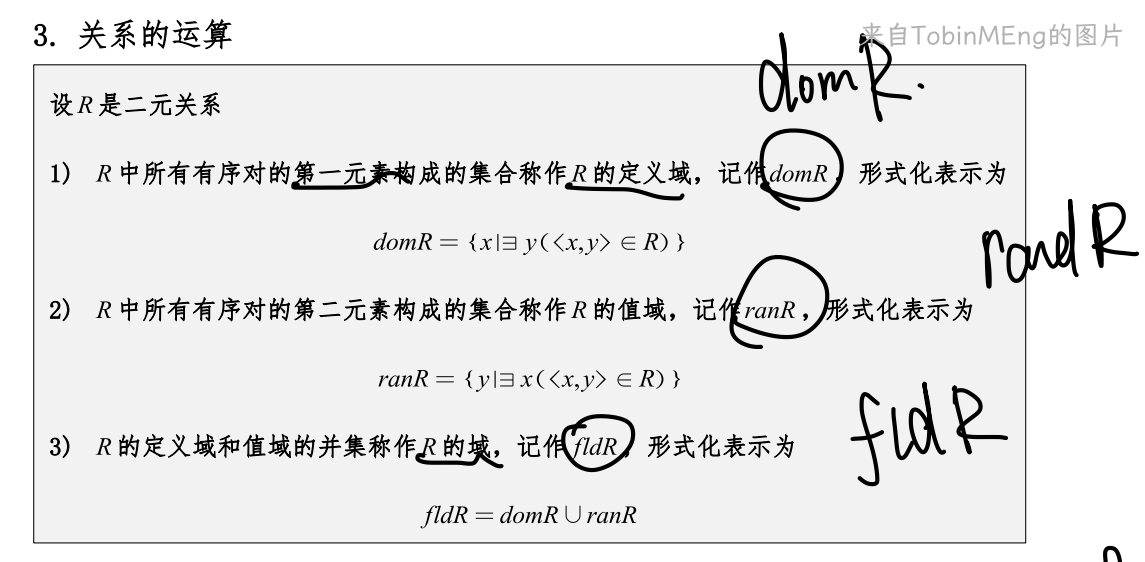
3、关系的运算
这里右复合和课本上正好相反。
课时八 二元关系
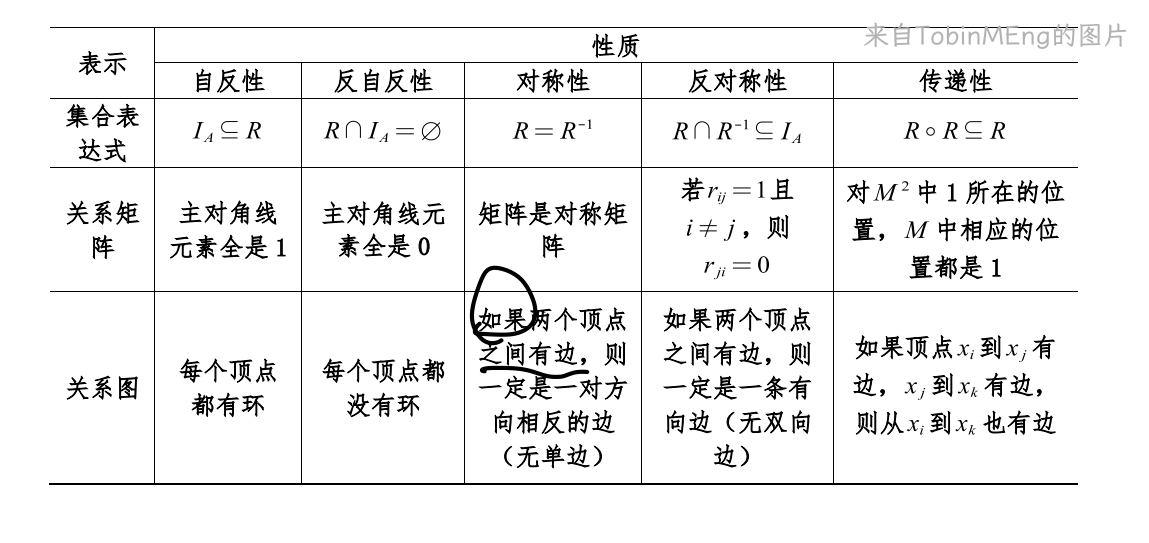
1、关系的性质
对称性是针对关系内的所有有序对,自反性也是针对关系内所有有序对的定义域的元素。
2、关系的闭包
关系的闭包其实就是在原关系的基础上,将原关系的所有自反(对称或传递)有序对加入进关系。所形成的大于等于原关系集合的一个有序对集合。
记住r是自反闭包,s是对称闭包,t是传递闭包。
3、有序关系与划分
等价类是一个集合,里面的元素是A上等价关系中dom是x的所有有序对的ran的值。
集合上的同余关系是一个等价关系
例题1:
划分其实就是一个集合通过一个划分得到了几个元素不重叠且完全使用所有的元素的子集族。
4、偏序关系
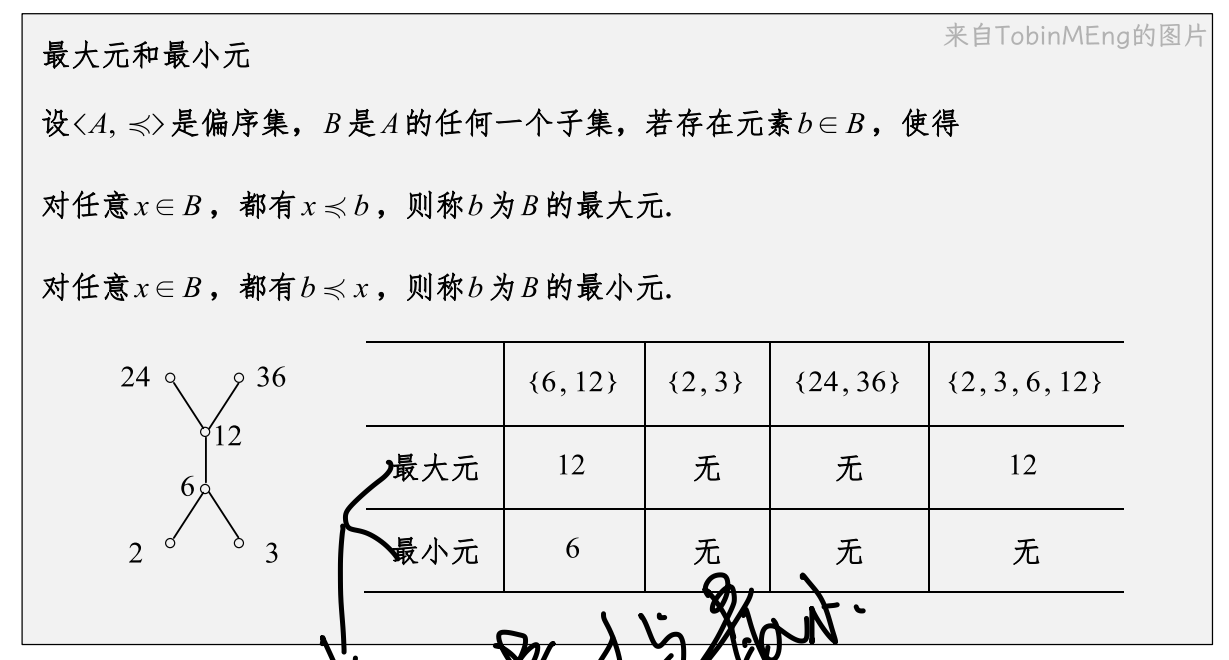
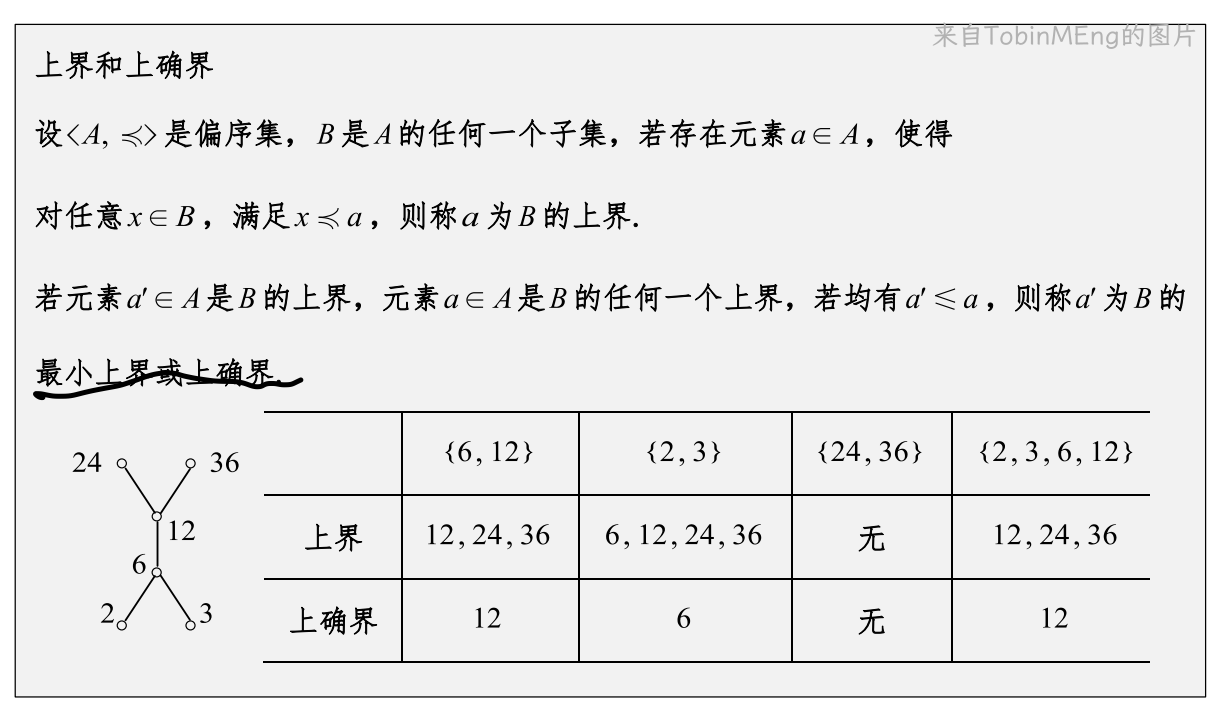
最大元和最小元和极大元和极小元可以直接看哈斯图得出。
对于最大元和最小元来说,应该是集合中元素在最上面层(下面层)且没有同层的那个元素,若有同层元素则不存在。
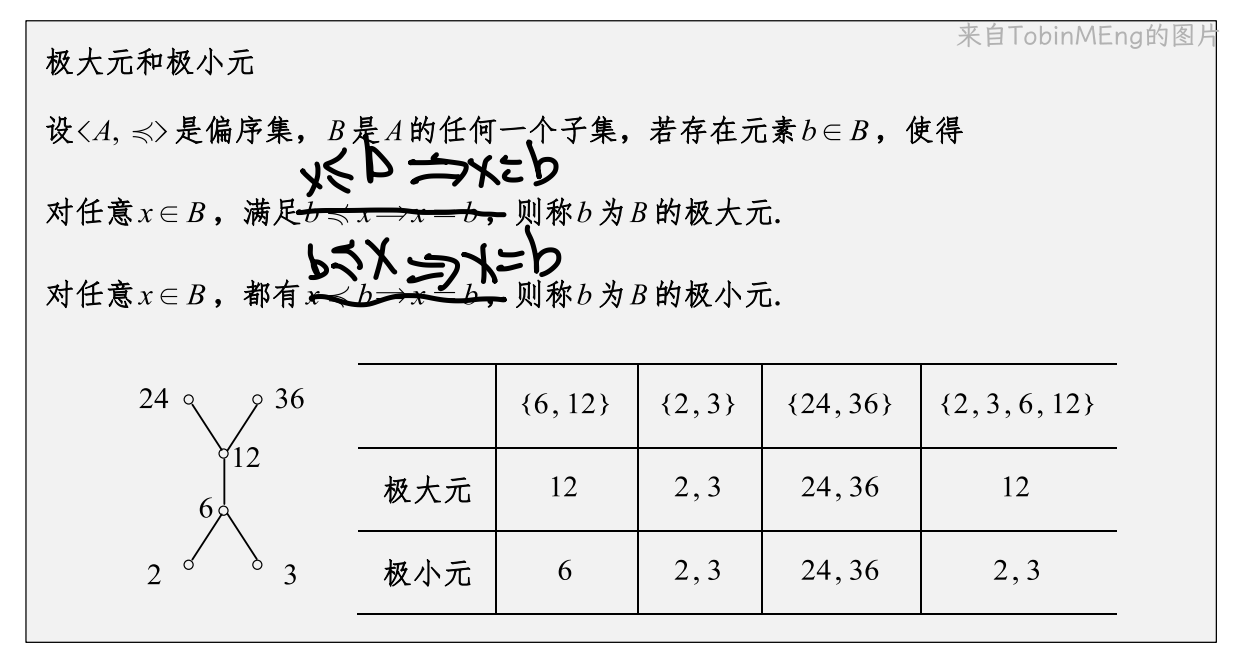
对于极大元和极小元来说,应该是集合中元素在最上面层(下面层)且没有同层的那一层的所有元素,都称为这个集合的极大元和极小元。
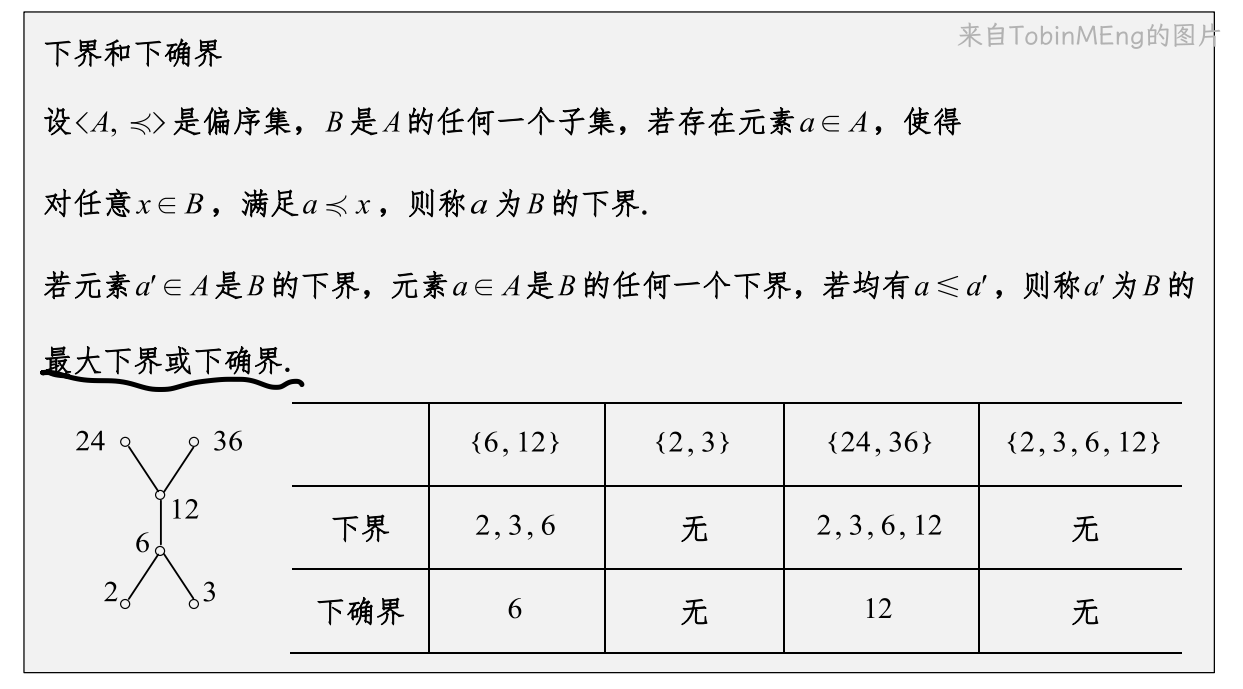
同样的上下界和上下确界的寻找也可以看哈斯图来理解:
上界和下届是:子集中最大或最小的那一层,如果是单独一个元素时,包含这个元素的所有上下元素就是这个子集的上下界。
上下确界是:子集中最大或最小的那一层,如果是单独一个元素时,则上下确界存在。界为最大或最小那一层的元素,否则上下确界不存在。
课时九 函数
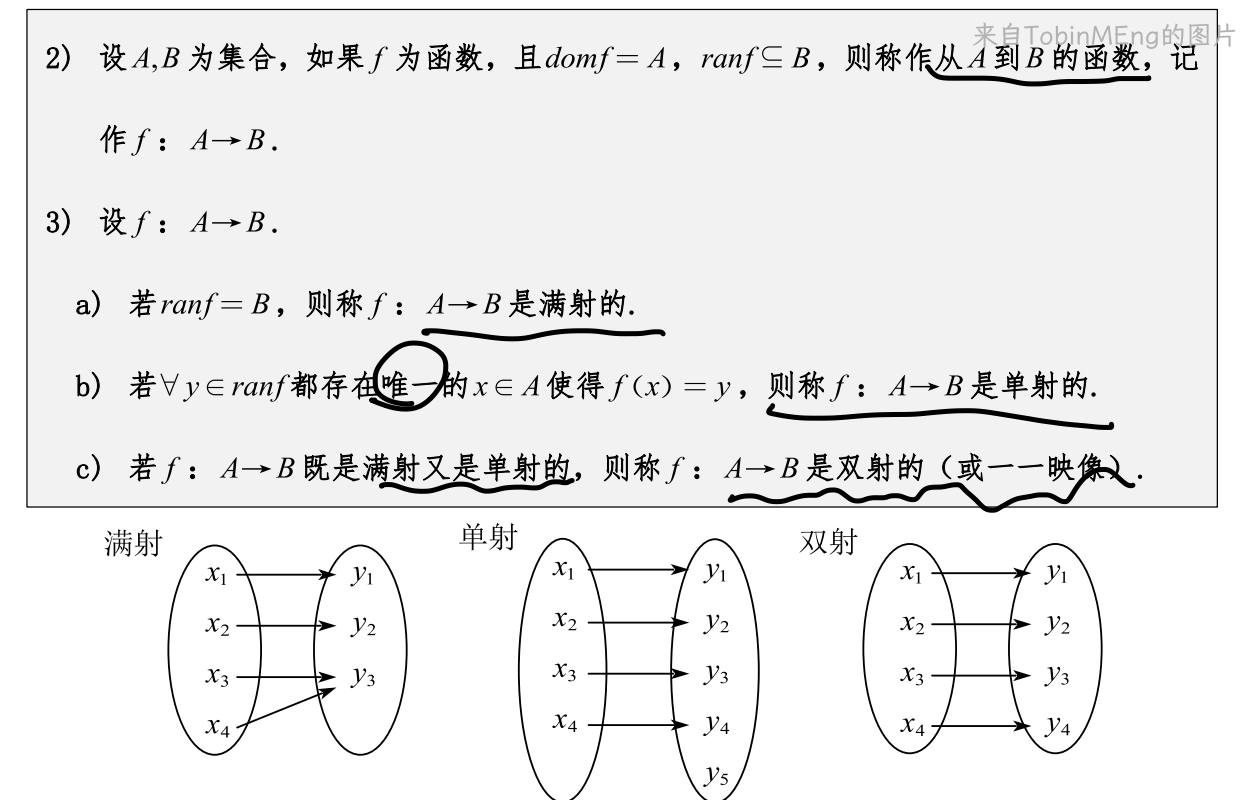
1、函数的定义与性质
例题1:
B的A次方称为B上A,是从A到B的函数。
2、函数的复合与反函数
函数其实就是一种特殊的关系,所以函数的复合与反函数其实就是关系的复合和反关系
课时十 代数结构
没讲
课时十一 图的基本概念
1、图
顶点数称作图的阶,n个顶点的图称作n阶图。
没有边的图叫做零图,1阶零图称作平凡图。注意n阶零图的符号表示为N右下小n
关联次数是边对两个顶点的次数。
桥(割边):对于无向图,如果删除了一条边,**整个图的联通分量数量变化,**则这条边称为桥
树的每一条边都是桥
割点:对于一个无向图,如果删除了一个顶点(顶点邻边也删除),整个图的联通分量数量改变,则称这个顶点为割点。
有向边的两个点都叫端点,有向边有始点和终点。
有向边的出度和入度。出度为d+,入度为d-。
握手定理:
无向图中,顶点的度数之和等于边数的二倍
有向图中,所有顶点的度数之和都等于边数的二倍,所有顶点的入度之和等于所有顶点的出度之和。等于边数
任何图中,奇度顶点的个数是偶数。
Δ(G)指的是图中最大的顶点的度数。
简单图指的是没有重边和自环的图。
无向完全图表示方法为K右下小n
2、通路与回路
3、图的联通性
图中两点是联通的的表示方法为u~v
无向图中任意两点之间都连通这样的图叫做连通图,否则叫做非连通图。
有向图中的联通性:
- 单向联通的
- 强联通的
- 弱联通的
强联通和单向联通都是在有向图中是联通的,只是强联通相当于无向边了,但是单向联通只是两点之间存在一个通路而已。
弱联通在有向图中就不连通,只是把有向边看做无向边之后才联通。
4、图的矩阵表示
第i行第j列表示顶点i与边j的关联次数,若j边是自环,则对应的ij的值为2,若i是j一个顶点,则为1,若j与顶点i不关联,则为0。
有向图的关联矩阵要默认有向图无环。
邻接矩阵表示为A(D),D为有向图,可以有重边。
重点!
邻接矩阵的n次幂的结果是从i到j长度为n的通路的个数。如果i等于j则为长度为n的回路的个数。
可达矩阵可以通过多次计算邻接矩阵的不同次幂来得到每两个点之间的联通性从而求得。
课时十二 欧拉图与哈密顿图
1、欧拉图
半欧拉图:有欧拉通路无欧拉回路
无向图:连通图 + 无奇度顶点
有向图:强联通 + 入度等于出度
2、哈密顿图
哈密顿图的判定是充分条件不是充要条件。
3、最短路问题
用dijkstra标号法求解最短路。
课时十三 树
1、无向树及其性质
2、最小生成树
Kruskal算法
3、根树及其应用
根树其实就是有向树
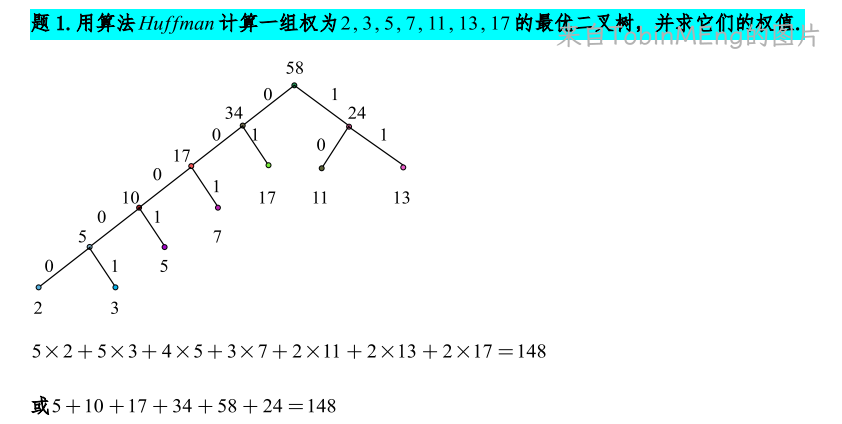
最优二叉树是Huffman树
例题1:
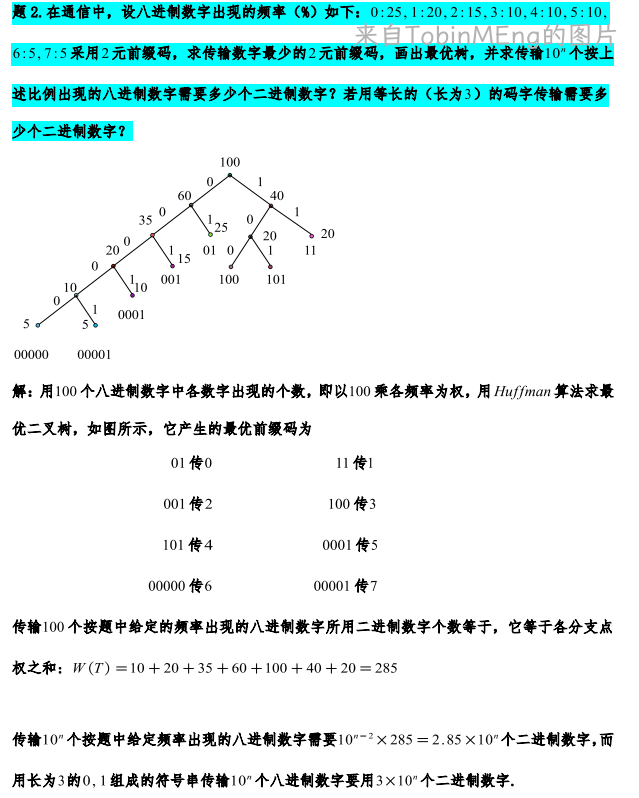
例题2:
课时十四 平面图
1、平面图的基本概念
二部图就是二分图
二分图的判定:图中不含奇环。
k5和k33不是平面图
2、欧拉公式
离散数学复习