密码学的数学原理
本篇文章用来记录密码学中用到的数学知识。
参考文献:
数论
基础知识
数论主要研究整数集合的性质,以及整数之间的关系。
- 良序性质:每个非空的正整数集合都有一个最小元。正整数集合是良序的,但是有些整数集合不是良序的,因为其中没有最小的元素,比如负整数集合、偶数集合等。根据良序性质,我们可以得到一个与之对称的关于负整数的性质:每个非空的负整数集合都有一个最大元。
- 定义1.1:若存在整数 p 和 q≠0 ,使得 r=p/q ,则称实数 r 是有理数,否则是无理数(所有整数 n 都是有理数,即整数是有理数的子集,因为有 n=n/1)
- 定义1.2:若数 x 是整系数多项式的根,即存在整数 a0,a1,…,an 使得 an x^n+an-1 x^(n−1+…+a0=0 ,则称数 x 是代数数,否则是超越数
- 定义1.3:取整函数 [x] 表示小于或者等于实数 x 的最大整数,有 [x]≤x<[x]+1,这表示整数 −[−x] 是大于或者等于实数 x 的最小整数。
- 推论1.1:对于任意实数 x 和整数 n ,都有 [x+n]=[x]+n
- 定义1.4:实数 x 的分数部分 {x} 表示 x,[x] 之差,即 {x}=x−[x]
- 推论1.2:对于任意实数 x ,都有 0≤{x}<1
- 定义1.5:若一个集合是有限的,或者集合是无穷的,但是与正整数集合之间存在一个双射,则称集合是可数的,否则是不可数的(有限集合都是可数的,不可数的集合都是无穷集合)
- 推论1.3:整数集合是可数的
- 定义1.6:对于a,b∈Z ,其中 a≠0 ,若存在 c∈Z 使得 b=ac ,则称 a整除 b , a是 b 的一个因子, b 是 a 的一个倍数,并且记为 a∣b ,否则称 a 不能整除 b ,记为 a∤b。(对于所有整数 n ,有 1∣n,n∣n)
- 定理1.4:若 a,b,c∈Z ,并且 a∣b,b∣c ,则有 a∣c
- 定理1.5:若 a,b,c,m,n∈Z ,并且 a∣b,a∣c ,则有 a∣(ma+nb)
- 定理1.6:若 a,b,c,d∈Z ,其中 a,c≠0 ,并且 a∣b,c∣d ,则有 ac∣bd
- 定理1.7:若 a,b,c∈Z ,其中 a≠0 ,则 a∣b 等价于 ac∣bc
- 定理1.8:若 a,b∈Z ,并且 a∣b ,则对于任意正整数 k 都有 a^k∣b^k
- 带余除法:若 a,b∈Z ,其中 b>0 ,则存在唯一的整数 r,q ,使得 a=bq+r ,其中 0≤r<b
素数和公因子
- 定义2.1:素数是大于 1 的正整数,并且只有两个正整数因子,合数是大于 1 的并且不是素数的正整数,即对于合数 n ,存在整数 a ,有1<a<n 并且 a∣n 。
- 定理2.1:所有大于 1 的正整数都有素因子
- 定理2.2:存在无穷多个素数
- 定理2.3:若整数 n 是合数,则 n 一定有不超过 根号n 的素因子
- 定理2.4:对于任意正整数 n ,存在至少 n 个连续的正合数
- 一个正整数的所有因子构成一个有限的集合,那么两个正整数的因子集合的交集就是这两个数的公共因子,能够同时整除这两个数,其中最大的那个公共因子非常重要。
- 定义2.2:不同时为零的整数 a,b 的最大公因子是指能够同时整除 a,b 的最大整数,记为 (a,b) 或者 gcd(a,b)。虽然任意非零整数都是 0 的因子,但是我们定义 (0,0)=0 。对于正整数 n 有 (n,0)=(n,n)=n 。对于整数 m 有 (m,1)=1
- 定义2.3:对于都不为零的整数 a,b ,若最大公因子 (a,b)=1 ,则称 a,b 互素。若有两个整数 p,q 并且 (p,q)=1 ,其中 p≠0 ,则分数 p/q 称为既约分数。
- 定理2.5:对于整数 a,b ,若 (a,b)=d>0 ,则有 (a/d,b/d)=1
- 推论2.2:若 a,b 为整数,并且 b≠0 ,则存在整数 p,q 互素,并且 a/b=p/q ,其中 q≠0
- 定理2.6:对于整数 a,b,c 有 (a+cb,b)=(a,b)
- 定义2.4:若 a,b 为整数,则其线性组合为 ma+nb ,其中 m,n 是整数
- 定理2.7:不同时为零的整数 a,b 的最大公因子是 a,b 的线性组合中最小的正整数
- 推论2.3:若 a,b 为整数,则存在整数 m,n 使得 (a,b)=ma+nb
- 推论2.4:两个整数 a,b 互素等价于存在整数 m,n 使得 ma+nb=1
群论
代数结构
如(G,*,#…)这个形式定义。需要注意的是:
- 集合G是非空的,必须要有元素。
- 运算必须是二元的。
若括号定义的这个东西加上一个性质,封闭性。就成为了代数结构(抽象代数中主要讨论的东西)。
封闭性的意思是,若集合G中的任意两个元素进行运算,结果跑不出该集合,结果仍然是这个集合中的元素。
群
定义:(G,*)是一个群,则它满足以下性质:
- 封闭性:任意a,b属于G,a * b 结果属于G。
- 结合律:任意a,b,c属于G,a * (b * c) = (a * b) * c。
- 单位元:存在单位元e,任意a属于G,a * e = e * a = a。
- 逆元:任意a属于G,存在b属于G,a * b = b * a = e,此时b称为a的逆元。
e的逆元是e的本身。逆元的意义是提供 * 的逆运算。
习惯地,(G,*)是一个群,通常简写为G是一个群。
群是抽象的概念,通过群的基本性质推出的性质是所有群共有的性质。
阶:
有限群:G是有限集,称G里元素的个数为群的阶。
无限群:G是无限集,群G的阶为无限阶。
单位元、逆元:
封闭性 =》 左单位元 = 右单位元 = 单位元
结合律 =》 左逆元 = 右逆元 = 逆元
定理:
定理1:群里的单位元是唯一的。(反证法可证)
群里只有一个元素时,称为“平凡群”。唯一元素就是单位元。
定理2:每个元素只有唯一的逆元。(反证法可证)
消去律:a * b = a * c =》 b = c。
方程a * x = b 有唯一解 x 属于G
(a * b )的逆元 等于(b的逆元 * a的逆元)
a的逆的逆 等于 a
阿贝尔群
又称 交换群。
- 定义:如果对于群G中的任意元素a,b属于G,都有a * b = b * a,则称G为阿贝尔群。
- 定理:群G是阿贝尔群,当且仅当,对于任意a,b属于G,有(a * b)的平方 等于 a的平方 * b的平方。
- 群的简记符号:a的t次方指的是t个a一起运算。t是整数,a是群元素。
- 定理:G是阿贝尔群,对于任意a,b属于G,有(a * b)的 t 次方 等于 a的t次方 * b的t次方。
子群
集合论中的集合和子集概念,其中子集扩展了集合的性质。同理群论中的子群概念扩展了群的性质。
定义:设G是一个群,H是G的子集,如果H是一个群,则称H是G的子群。
平凡子群:({e}, )、(G,\)。单位元群和群G本身都是群G的平凡子群。
非平凡子群:(H,*)且H 不等于 {e}和G(又称真子群)
定理:H是群G的子群,e属于G是单位元,则e也是子群H的单位元(群的单位元也是其子群的单位元)
定理:H是群G的子群,a属于H,则a的逆也属于H。
判断子群定理(1):H是群G的非空子集,对于任意a,b属于H,都有a * b的逆属于H,则H是G的子群。
该定理其实是证明了H满足1.非空子集,2.封闭性,3.结合律,4.单位元,5.逆元 五个性质。
判断子群定理(2):H是群G的非空子集,如果H是有限集,而且G的运算*在H上满足封闭性,则H是G的子群。
其实子群指的是 群 的特殊的非空子集。 群G的非空子集H,若对G的乘法也成为群,则称H为G的子群。
子群的构造
针对阿贝尔群:
定理(1):G是阿贝尔群,m属于Z,则G的m次方是G的子群。
例子:
- (Z*_p)的平方,即整数在模p(奇素数)的平方群是(Z*_p)的子群。
- (Z*_n)的m次方,即整数在模自然数n的m次方群是(Z*_n)的子群。
- mZ是Z的子群。
- mZ_n是Z_n的子群。
定理(2):G是阿贝尔群,m属于Z,则G中所有元素的m次方等于e的元素构成的群G{m}是G的子群。
例子:
- 构造Z_n的子集Z_n{m}:设d = gcd(n, m),使得mZ同余0modn,可得Z同余0mod(n/d),即为{0,n/d,2n/d,3n/d…}。考虑Z_n{d},根据定义可知,z属于dZ同余0modn集合,即也为{0,n/d,2n/d,3n/d…}。即Z_n{d} = Z_n{m} = (n/d)Z_n {d = gcd(n, m)}
性质:Z_n{d} = Z_n{m} = (n/d)Z_n {d = gcd(n, m)}
对于Z_p群来说,例如Z_15群,其子群中通过两种定理构造的子群存在关联,对于定理(1)来说,构造出来的5Z_15子群就和Z_15{6}子群是相等的。
整数群的子群
定理1:H是Z的子群,则存在唯一的负整数m,使得H=mZ。
定理2:m1和m2是非负整数,则m2是m1的因数,当且仅当,m1Z是m2的子集。
例子:27Z包含于9Z包含于3Z包含于Z。
定理3:H是Z_n的子群,
- 存在n的唯一正因子m,使得H = mZ_n。
- m1和m2是n的正因子,则m2是m1的因子,当且仅当,m1Z_n 包含于 m2Z_n。
子群构造子群
用子群来构造新的子群。
定理(1):H1和H2是阿贝尔群G的子群,则H := H1H2也是G的子群,其中H := H1H2 := {a1 * a2 | a1属于H1, a2属于H2}
注意:通常H1H1 ≠ 2H1。例如Z + Z = Z,但是 Z ≠ 2Z。即 Z + Z ≠ 2Z
扩展:H1,…,Hn是阿贝尔群G的子群,则H1…Hn也是G的子群。
定理(2):H1和H2是群G的子群,则H := H1∩H2也是G的子群。(即子群的交集也是子群)(该方法没有限制阿贝尔群,因为证明时没有用到交换律)
扩展:H1,…,Hn是阿贝尔群G的子群,则H1∩…∩Hn也是G的子群。
子群的并集未必是子集,例如:2Z∪3Z就不是一个子群,因为2+3=5,而5不在2Z∪3Z中,不满足封闭性。
定理(3):H1和H2是G的非平凡子群,则G≠H1∪H2。
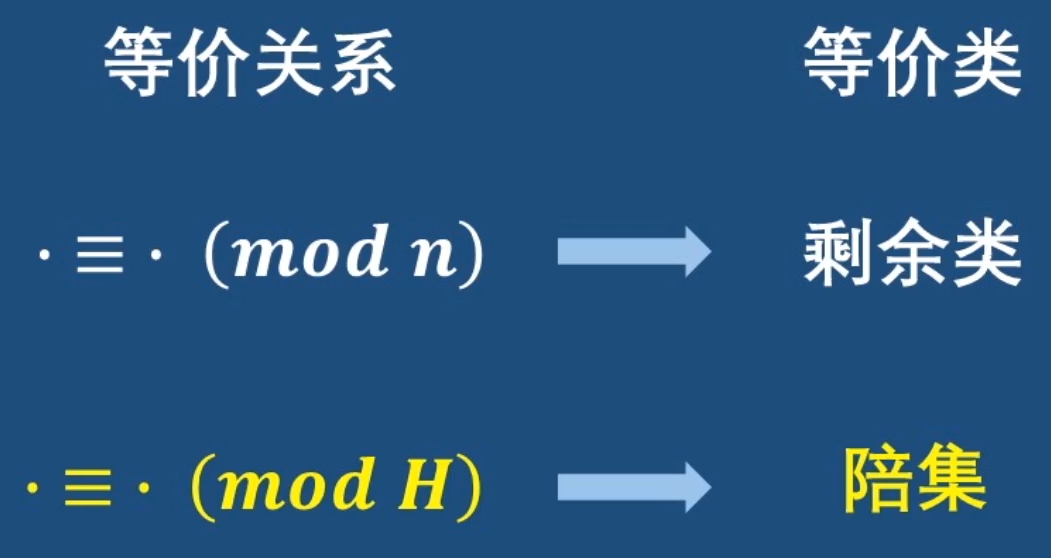
陪集
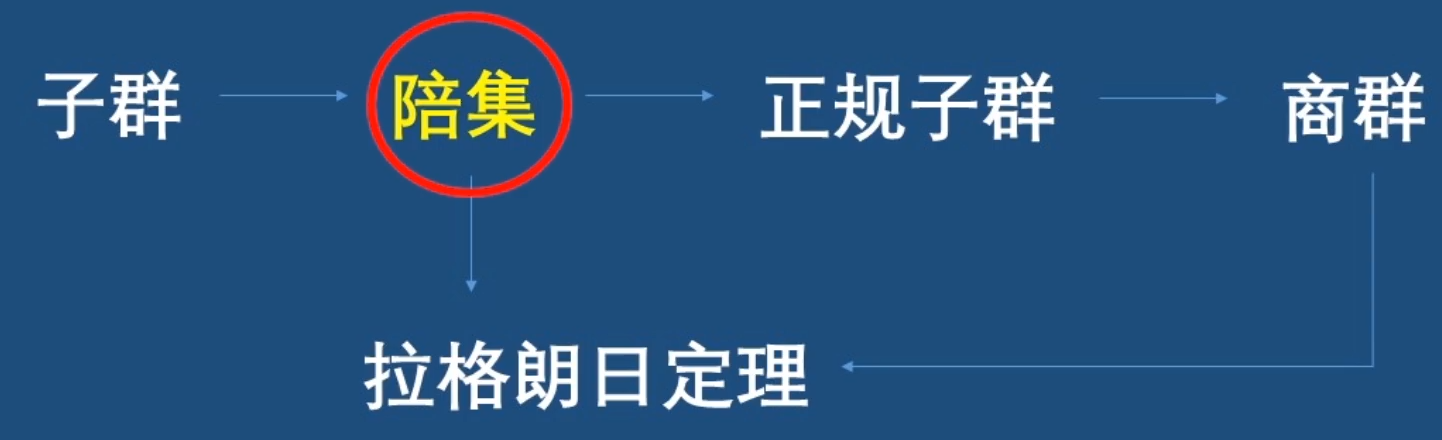
- 定义:H是群G的子群,a属于G,则aH := {a * h |h属于H}称为H关于a在G中的左陪集。同理,Ha := {h * a|h属于H}称为H关于a在G中的右陪集。如果aH = Ha,称为H关于a在G中的陪集。a称为代表元。陪集的表示方法:[a]H
- 性质1:a属于[a]H
- 性质2-1:[e]H = H (平凡陪集)
- 性质2-2:若a属于H,当且仅当,[a]H = H
- 性质3:[a]H = [b]H,当且仅当,(a的逆 * b)属于H
拉格朗日定理
由陪集的性质3可知,若b = a * h,h属于H,此时a和b会被分配在同一个陪集中。
引入二元关系符号≡,式子:a≡b(mod H)表示a和b在同一个(由H构造)的陪集里。

所以[a]H的含义可以为:1.以a为代表元的陪集,2.a和H构造的陪集,3.H为分类依据时,a被分配到的陪集。
- 性质:任意两个陪集[a]H和[b]H之间存在双射。任意陪集[a]H和子群H是等势的。(即子群H构造的陪集的大小和子群H是相等的)
- 定理:G是有限群,H是G的任意子群,则|H| ||G|,即H内元素的个数必须是G内元素的个数的因数。
商群
正规子群:
- 定义:设N是群G的子群,如果对于任意a属于G,都有aN = Na,称N为G的正规子群。
商群:
- 定义:集合G/N := {[a]N | a属于G},即由正规子群N构造的所有陪集。定义陪集间二元运算[a]N * [b]N := [a * b]N,即两个陪集的单位元先进行群G的二元运算*之后再构造群G的陪集。该集合为一个群,(G/N,*)。叫做群G在模N下的商群。
- 商群G/N的阶:[G:N]表示商群G/N的阶。
- 定理(1):G是有限群,N是G的正规子群,则[G:N] = |G| / |N|
- 定理(2):G是有限群,N是G的正规子群,K是N的正规子群,则[G:K] = [G:N][N:K]
阿贝尔群:
性质(1):H是阿贝尔群G的子群,对于任意a属于G,有aH = Ha (=[a]H)
注意:如果对于任意a属于G,都有aH = Ha,则G未必是阿贝尔群。
性质(2):阿贝尔群的子群都是正规子群。
性质(3):阿贝尔群的任意子群都可以构造商群。
性质(4):阿贝尔群的子群构造的商群也是阿贝尔群。
群同态
群同态本质上就是定义在群和群之间的映射,或者说函数,但是是一种特殊的函数。需要满足映射完的元素还可以进行运算。
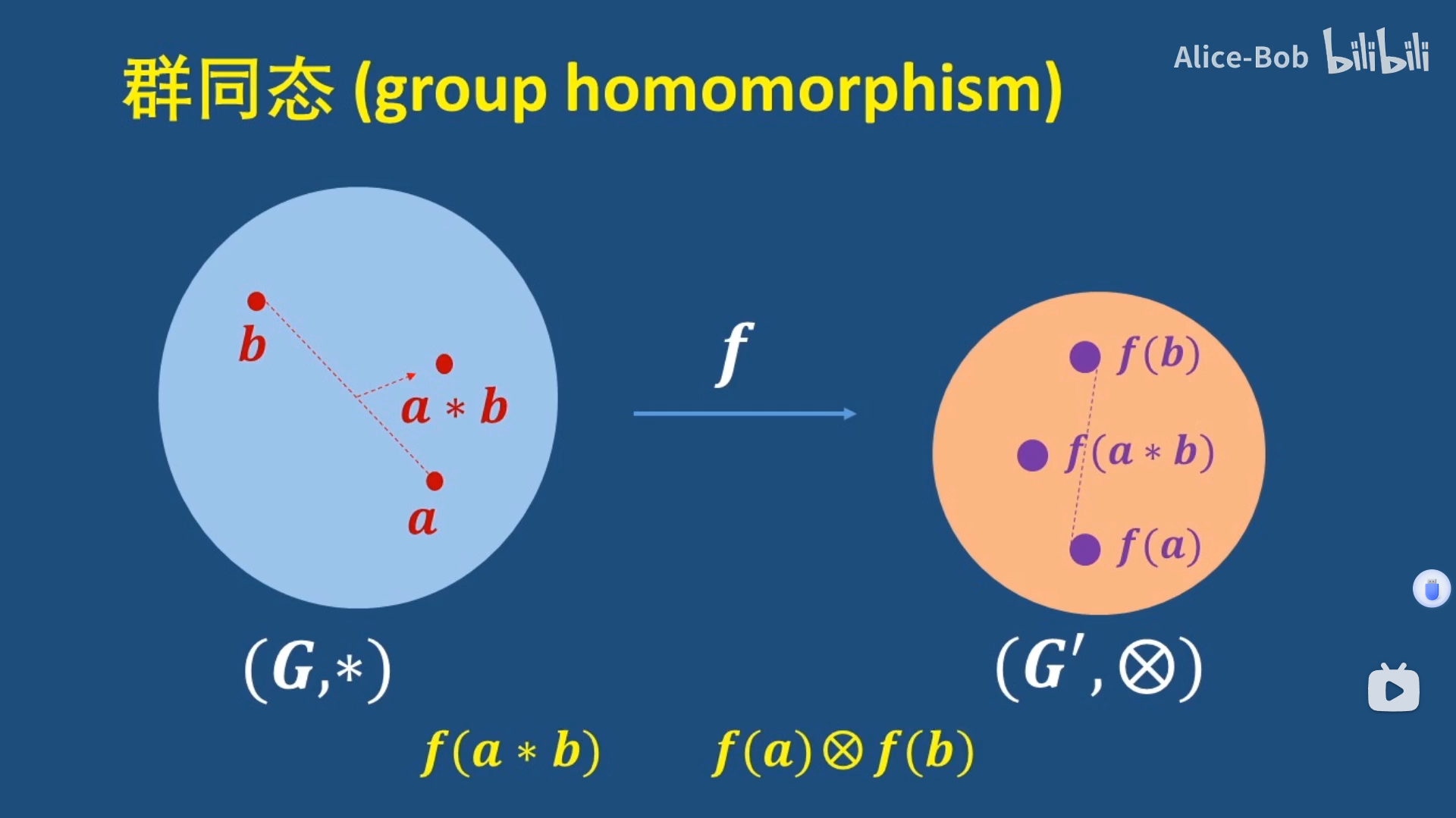
定义:设群(G,*)和群(G’,x),如果函数f: G -> G’对于任意a,b属于G,都有 f(a * b) = f(a) x f(b),则称f为群(G,*)和群(G’,x)的群同态。(群同态可能有多个,可能不唯一)
判断两个群是否群同态只需检验 f(a * b) = f(a) x f(b) 即可。
同态像:有些元素经f映射之后的落点可能只是G‘的子集,也就是说G’中的一些元素在G中可能找不到原像。那些G‘中可以找到原像的那些元素构成的子集叫做同态像。记为Im f。Im f := f(G) := {f(a) | a 属于 G}
同态核:记为Ker f。G中经过f映射后等于G’中单位元的那些元素就是核里的元素。Ker f := {a 属于 G | f(a) = e’} (e’代表G’中的单位元)
嵌入映射:子群到群的嵌入映射是个群同态。f(a) = a。并且原像到像之间是一对一的。
单一同态:f是单射。
自然映射:G到G/N的映射,N是G的正规子群,G/N是对G中元素的划分,则f(a) = [a]N即将G中的每个元素划分进相应的陪集。这个函数就是一个群同态。定义域是G,值域就是对应的商群。
其中N也是G/N商群的元素,称为平凡陪集。所以,自然映射的同态核就是正规子群N。
自然映射的例子:Z/nZ,其核就是正规子群nZ。
满同态:f是满射。
m次方映射:对于阿贝尔群G,设f(a) = (a)^m。则f是m次方映射,也是一个同态。Im f = G^m,Ker f = G{m}。
雅可比映射。
群同态的性质
性质(1):f(e) = e’ (e和e’分别是群G和群G’的单位元)
性质(2):f(a的逆元) = f(a)的逆元,任意a属于G。
性质(3):H是G的子群 => f(H)是G‘ 的子群。
扩展:H := G => f(G) = Im f (同态Im f 是G的子群)
性质(4):H’是G’的子群, => f的逆运算(H’) 是G的子群。f的逆运算表示求H’的原像集合。
性质(5):f(a^m) = f(a)^m
结论:同态核Ker f 是G的子群,同态像Im f是G‘的子群。
群同态的复合
- 定理:f是(G,*)到(G’,x)的群同态,f’是(G’,x)到(G’’,田)的群同态,则f和f’的复合 f’of: G -> G’’也是群同态。
同态核的穿越
- 定理:f: G - > G’是群同态,则Ker f是正规子群。
如何判断单一同态
- 定理(1):f: G ->G’ 是群同态,任意a,b属于G,有f(a) = f(b),当且仅当,a 同余 b (mod Ker f)。
- 定理(2):f: G - >G’是群同态,有f是单射,当且仅当,Ker f = {e}。
判断方法
- f是单一同态,当且仅当,Ker f = {e}。
- f是满同态,当且仅当,同态像Im f = G。
第一同构定理
- 双射:既是单射又是满射
- 若一个群同态是一个双射函数,它就叫群同构。(群同构是一种特殊形式的群同态)。
- G与G‘同构,指G到G’之间存在一个群同构。群同构也可以定义在自身上,G到G的同构,称为G的自同构。
- 群同构的意义:指群同构的群,本质上是同一个群。所以只需研究其中一个群的性质即可。
第一同构定理(又称,基本同态定理):
定理:设群(G,*)和群(G’,x),f:G->G’是群同态(同态核是Ker f,同态像是Im f)。
则G/ Ker f 同构与 Im f,其中同态运算ρ: [a]Kerf -> f(a),该运算ρ是将商群里的陪集映射成代表元的像。
理解:G/ Ker f 这个商集其实是对于同态f的同态核求的剩余类,而该剩余类的代表元进行f同态运算之后得到的就是Im f。第一同构定理告诉我们,同态核构造的商群和同态像是同构的。
若将同态运算进行修改,ρ’ : G/Ker f -> G’ ,ρ’ 可能不是满射,但是可知ρ’ 是单一同态。
循环群
构造子群的一种方法:
- 定理:设G是群,a属于G,则<a> := {a^z | z∈Z}是由a生成的G的子群。
循环群的概念:
- 定义:设G是群,g属于G,如果G = <g>,则称G是循环群,g是循环群G的生成元。
- 例子
- 整数群Z是加法循环群。记为<1>,<-1>
- mZ是加法循环群。记为<m>,<-m>
- Z*_5是乘法循环群。记为<2>,<3>
- 循环群根据元素是否是有限的可分为:无限循环群和有限循环群。
- 一个循环群可能有很多生成元。有限循环群的生成元个数是可以计算的,任意无限循环群都只有两个生成元。
- 定理(1):任意循环群都是阿贝尔群。
- 定理(2):循环群的子群是循环群。
- 定理(3):设G是循环群,H是其子群,则商群G/H是循环群。设G的生成元为g,则G/H的生成元就是[g]H。
密码学的数学原理


