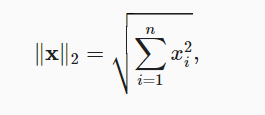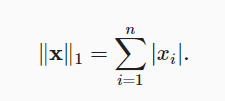深度学习<Dive into deep learning>_2预备知识
所有笔记和教程都使用Pytorch框架来实现
本系列博客来自于: DIVE INTO DEEP LEARNING,李沐老师的课,Orz
2.1数据操作
1 | |
运算符:
标量运算符:按照元素进行运算。
对于具有相同形状的张量,常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算
包括一些标量运算函数:torch.exp()
同时可以使用torch.cat将两个张量连接在一起形成一个张量
同时可以使用==或者其他的比较运算符来实现张量中的标量的比较运算
X.sum()可以实现张量中所有元素的求和
1 | |
广播机制:
对于形状不相同的张量,可以使用广播机制来对这两个张量进行运算
矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。
索引和切片:
-1表示数组中最后一个元素,同时可以使用切片来取数或者批量的赋值
节省内存:
Python中默认的Z = X + Y生成的结果会新产生一个对象,原来的Z张量内存就被浪费掉了,为了避免这种情况发生,可以使用Z[:]来解决
对象的转换:
2.2数据预处理
数据的处理一般采用pandas来实现
数据的读取:
对于csv(逗号分隔值)文件数据:
1 | |
处理缺失值:
一般的“NAN”表示缺失值,一般处理缺失值的方法有:插值法和删除法。
位置索引iloc可以将数组分为若干部分。其中fillna表示填充数据中的NAN数据,inputs.mean()表示数据中每一列的均值。
1 | |
对于离散值或者类别值,pandas可以将这一列中的所有类别拆分成若干列,并通过标记0和1来表示该行记录是哪一个离散值
转换为张量格式:
通过torch.tensor将数值类型转换为张量类型。
2.3线性代数
标量是只有一个元素的张量,
向量是一维的张量
对于向量来说,向量的维度为向量的长度。(然而,张量的维度用来表示张量具有的轴数。)
矩阵是向量从一阶推广到二阶的结果。
矩阵具有相同数量的行和列时,它被称为方阵
交换矩阵的行和列时,结果称为矩阵的转置
对称矩阵是方阵的一种特殊类型,对称矩阵等于其本身的转置
张量是矩阵的推广,张量具有任意数量的轴
张量的按元素一元运算不会该表张量的形状,相同形状的两个张量按元素运算的结果也是相同形状的张量
两个矩阵的按元素乘法称为Hadamard积(数学符号⊙)
将张量乘以或加上一个标量,不会改变该张量的形状,其中张量的每个元素都会与标量相加或相乘
降维:
对张量进行求和可以对张量实现降维。比如对张量进行整体求和,就是将张量沿所有的轴减低张量的维度,使其称为一个标量
我们还可以指定张量按照某一个轴进行降维
对于矩阵来说,行的轴是轴0,若对行进行降维后,行这一轴就会消失,同理矩阵的列是轴1。
若对一个矩阵沿一个维度降维,无论是行还是列,降维的结果都将是一个向量即一个行向量,若要沿列降维后得到一个列向量,需要使用非降维求和 ,这样的求和还会保持原来矩阵的形状(行数),这样方便后续进行广播操作。
1 | |
均值:
平均值常常通过总和除以元素总数来计算。
均值也可以沿指定轴降低张量的维度
1 | |
点积:
点积是两个向量之间的操作。
点积就是两个向量相同位置的按元素乘积的和
对于向量点积来说,由于没有行向量和列向量的区分,我们可以直接将两个向量按元素进行乘法,然后对结果向量进行求和。
向量的点积可以计算值的加权和或者加权平均,或者夹角的余弦
矩阵-向量积:
矩阵向量积中的向量常常指的是列向量。
一个m*n的矩阵和一个维度为n的向量的矩阵向量积的结果是一个维度为m的列向量
我们可以把矩阵向量积看为一个维度为n的向量向维度为m的向量的一个转换。构造一个矩阵可以协助向量进行转换。
矩阵-矩阵乘法:
矩阵矩阵乘法指的是一个mk的矩阵和一个k\n矩阵之间的矩阵乘法。
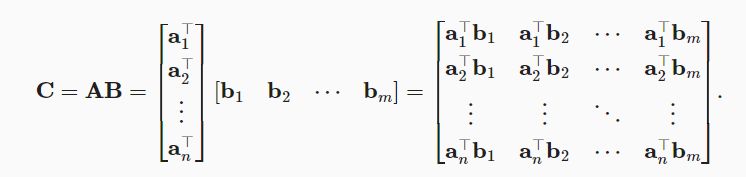
image-20221103093536910
范数:
范数为了表示一个向量的大小,这里的大小不是维度,而是分量的大小。
范数有一些性质:
- 对向量进行成倍缩放,该向量的范数也会成倍的缩放
- 三角不等式,两个向量的和的范数应该小于等于两个向量范数的和
- 范数应该是非负的
欧几里得距离被称为L2范数,L2范数是向量元素平方和的平方根:
常常使用中L2范数会忽略下标2
在深度学习中,比较经常的使用L2范数的平方
L1范数,指的是向量元素的绝对值之和:
与L2范数相比,L1范数受异常值的影响较小
与向量相似,矩阵的Frobenius范数是矩阵元素的平法和的平方根,Frobenius范数满足向量范数的所有性质。
1 | |
范数的意义:
在深度学习中,我们常常解决最优化问题,要最大化或最小化某一个指标,其中向量之间的距离即目标,就是范数。
2.4微积分
深度学习<Dive into deep learning>_2预备知识