深度学习初探

暑假学习深度学习课程的一些小小总结

二分分类

什么是Logistic 回归？

logistic 回归函数：来对一组输入做一个 0 ~ 1 的概率判断。

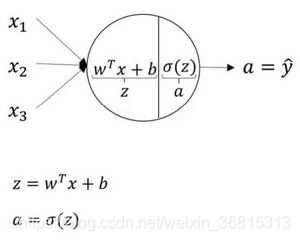
x为输入的特征向量，得到的回归函数值为 sigma(w^(T) * x + b) ，参数为w和b，是一个在0和1中间的一个概率。sigma(z) 是 1 / 1 + e ^ (- z) 。

损失函数：lost(y^, y) = - ( y log y^ + (1 - y) log(1 - y^) ) （其中y^为y的预测值）。越小越好。

成本函数：J(w, b) = 1 / m * Σ lost(y^, y) = -1 / m * Σ(y log y^ + (1 - y)log(1 - y^)) 。为m组损失函数的平均值，越小越好。

梯度下降法：w := w - αd(J(w, b)) / d(w) ，b := b - αd(J(w, b)) / d(b) 。α是学习率。

梯度就是函数对变量的偏导。

正向传播：用参数计算出函数的值

反向传播：利用函数来计算每一个参数的导数

对Logistic 回归的一组数据进行梯度下降法：

Logistic 回归的Python实现

对Logistic 回归的m组数据进行一次梯度下降法：

J = 0; dw1 = 0; dw2 = 0; db = 0;
for i = 1 to m
    z(i) = wx(i)+b;
    a(i) = sigmoid(z(i));
    J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));
    dz(i) = a(i)-y(i);
    dw1 += x1(i)dz(i);
    dw2 += x2(i)dz(i);
    db += dz(i);
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;
w = w - alpha * dw
b = b - alpha * db

如何减少循环的次数？

使用向量化来减少显式For循环。

import numpy as np #导入numpy库
a = np.array([1,2,3,4]) #创建一个数据a
print(a)
import time #导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) #通过round随机得到两个一百万维度的数组
tic = time.time() #现在测量一下当前时间
#向量化的版本
c = np.dot(a,b) #对a，b进行矩阵乘法
toc = time.time()
print(“Vectorized version:” + str(1000*(toc-tic)) +”ms”) #打印一下向量化的版本的时间
#继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
    c += a[i]*b[i]
toc = time.time()
print(c)
print(“For loop:” + str(1000*(toc-tic)) + “ms”)#打印for循环的版本的时间

通过使用numpy中的函数来进行向量运算从而减少显式For循环。

可以使用向量化完全消除显式的For循环：

Z = np.dot(w.T, x)+b
A = σ(Z)
dZ = A − Y
dw = 1 / m ∗ X ∗ dZ.T
db = 1 / m ∗ np.sum(dZ)
w = w − α ∗ dw
b = b − α ∗ db

现在我们利用前五个公式完成了前向和后向传播，也实现了对所有训练样本进行预测和求导，再利用后两个公式，梯度下降更新参数。我们的目的是不使用for循环，所以我们就通过一次迭代实现一次梯度下降，但如果你希望多次迭代进行梯度下降，那么仍然需要for循环，放在最外层。不过我们还是觉得一次迭代就进行一次梯度下降，避免使用任何循环比较舒服一些。

学习进度：吴恩达深度学习课程第一课前两周课（24节）

浅层神经网络

什么是双层神经网络？

神经网络的大致组成：输入层，隐藏层，输出层。

logistic 回归只有输入层和输出层。

双层神经网络的两层是指隐藏层和输出层，输入层不算。（也可以叫单隐层神经网络）

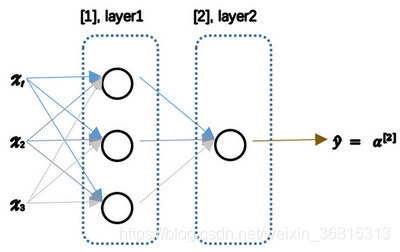
上图是一个双层神经网络的示意图。

对比一般的Logistic 回归，对于一组输入来说，双层神经网络有多个a在第一层的输出到第二层去。在输出层中，输入是隐藏层中运算得到的a值，输出是经过Logistic 回归得到的最终值。

上图是隐藏层中一个神经元的具体构造。

同时我们也希望可以将这个双层神经网络进行向量化从而来简化我们的运算。

如何将双层神经网络进行向量化？

该图将一组数据进行了向量化，通过上图的运算，可以更快地得出一组数据经过一次双层神经网络处理的结果。

如图的操作可以将多组数据进行向量化运算，即，经过一次操作对多组输入进行一次双层神行网络处理。

如何选择激活函数？

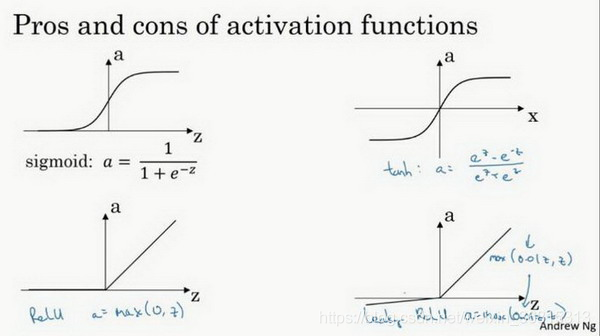
常见的激活分类有：σ函数，tanh函数，ReUL函数，Leaky Relu函数。

对于tanh函数，是由σ函数向下平移和伸缩后得到的。相比于σ函数，数据的平均值更接近0，这会使下一层学习简单一点。

选用适合的激活函数可以加快机器学习的速度，常用的Relu函数的优点如下：

第一，在 z 的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个if-else语句，而sigmoid函数需要进行浮点四则运算，在实践中，使用ReLu激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。

第二，sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0，这会造成梯度弥散，而Relu和Leaky ReLu函数大于0部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的稀疏性，而Leaky ReLu不会有这问题)

z 在ReLu的梯度一半都是0，但是，有足够的隐藏层使得z值大于0，所以对大多数的训练数据来说学习过程仍然可以很快。

概括一下不同激活函数的过程和结论：

sigmoid激活函数：除了输出层是一个二分类问题基本不会用它。

tanh激活函数：tanh是非常优秀的，几乎适合所有场合。

ReLu激活函数：最常用的默认函数，，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLu。公式 a = max( 0.01 z , z ) 为什么常数是0.01？当然，可以为学习算法选择不同的参数。（注意ReLu函数是非线性的）

注意：在选择激活函数的时候，要选择非线性函数，因为多层线性函数的组合得到的结果还是线性的，那么神经网络只是把输入线性组合再输出。只有在做机器学习中的回归问题的时候才可能会选择线性函数作为激活函数。

激活函数的导数

对于常见的几种激活函数的导数：

sigmoid函数 **σ(x) = a 的导数为 **a (1 - a)

tanh函数 tanh(x) = a 的导数为 1 - a^2

Relu函数 max(0, x) = a 的导数在 x < 0 的时候为0， 在 x > 0 的时候为1，在 x = 0 的时候没有定义，一般手动定义为 0 或者 1 。

Leaky Relu函数 max(0,01x, x) = a 的导数在 x < 0 的时候为 0,01 ， 在 x > 0 的时候为1，在 x = 0 的时候没有定义，一般手动定义为 0 或者 1 。

双层神经网络的梯度下降法（反向传播的实现）

由以上学习可知双层神经网络的正向传播就是按照所给的基本公式进行计算，而反向传播可以在每一轮中对模型中的参数进行调整。

反向传播与普通Logistic回归不同的地方在于计算第一层的dz时的差别。

这里np.sum是python的numpy命令，axis=1表示水平相加求和，keepdims是防止python输出那些古怪的秩数 ( n , )，加上这个确保矩阵 db[ 2 ] 这个向量输出的维度为 ( n , 1 ) 这样标准的形式。

随机初始化

为什么在Logistic回归中不能将W数组的初始化定为0？

因为这样的话在第一层中的神经元就会计算出相同的结果，这样